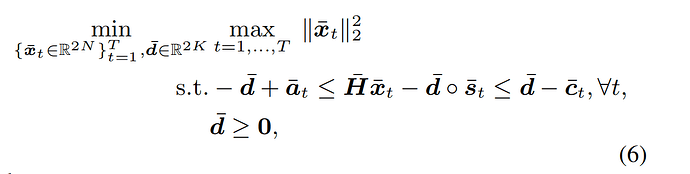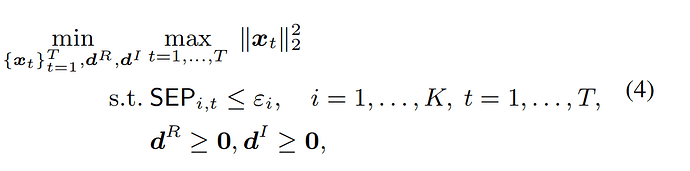Hi I want to solve the formula-9 in CVX, so I write the code like the following.
cvx_begin
cvx_precision best
variable u_bar(2*K,T);
variable d_bar(2*K,1);
reform_power = (d_bar(:,1).*bs(:,1)+ u_bar(:,t))' * bR * (d_bar(:,1).*bs(:,1)+ u_bar(:,t));
minimize reform_power;
subject to
%------------
%u_bar(i,t) >= -d_bar(i,t) + a_bar;
%u_bar(i,t) <= d_bar(i,t) - c_bar;
%--------------
for i=1:2*K
if bs(i,t) == 1 || bs(i,t) == -1
abs(u_bar(i,t)) <= d_bar(i,1) - c1;
elseif bs(i,t) == 3
u_bar(i,t) >= -d_bar(i,1) + c2;
elseif bs(i,t) == -3
u_bar(i,t) <= d_bar(i,1) - c2;
end
d_bar(i,1) >= 0;
end
cvx_end
if peak_power_pre <= reform_power
peak_power_pre = reform_power;
else
break;
end
I wonder is that part actually do the work shown in formula-9,since there is a gap between cvx results and the answer offered in the original paper.
I don’t see a correspondence between your code and the paper’s solution method.
At high level, the paper’s method is to solve the 2nd optimization problem, and then post-process the optimal u_t (for t from 1 to T) and d to produce the optimal x_t per the 3rd line of Proposition 1.
You don’t seem to have max over t in the objective function. Then you need to minimize that. I.e., minimize(max(...)) , where ... is the collection of convex quadratic objective terms for t from ` to T.
I have no idea what you’re doing with the constraints with all the separate logic depending on the value of t.
I think you might want to declare u as an n by T variable, where n is the number of elements of d. You can index in to the correct t value each time you use it.
Perhaps you need to use a for loop to build up the argument of the max in the objective, using quad_form to form each quadratic term within the max. The constraints should be easily vectorizable using repmat, which would save CVX processing time.
There might be more you need to do, but start with this, and reexamine everything you did.
I don’t understand the purpose of the method seemingly implied by Proposition 1. That is because the original problem appears to be a convex optimization problem (SOCP) which may be as easy or easier to solve than the 2nd problem, and doesn’t require the post-processing.
I cannot agree more. However, it is a custom designed precoding provided by the paper. It is a SEP-constrained symbol power problem. In a MIMO system, the received signal is
y_i,t = H_i * x + v_i,t
where s is drawn from a QAM constellation
S_i = {s_R + js_I}
The goal is to achieve formula 2, which ensures Information can still be identified even in the presence of interference from multiple users. Under SEP constrained, the formula becomes formla-4
And I suppose it only need to fine a t for the peak power after a minimization by cvx. However, the result is not what I want.
You can start by correctly implementing the method in the paper. As I pointed out in my first post, you clearly did not do so in your first post.
Thank you. Actually, I do not know how to achieve the minmax expression in the cvx, this has been troubling me for many days.
This is an example minimizing the maximum of quadratic form terms.
cvx_begin
variable x(3)
max_argument = 0;
for k=1:10
max_argument = [max_argument;quad_form(x,A(:,:,k))];
end
minimize(max(max_argument))
% add constraints
cvx_end
The nasic idea id the objective needs to be minimize(max(...)) where .... is the collection of terms over which the (inner) max takes place.