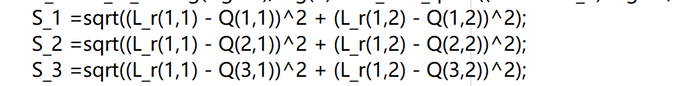Use norm.
S_1 = norm([L_r(1,1)-Q(1,1);L_r(1,2)-Q(1,2)])
If you want to get fancier, you can use norms with a matrix argument, and calculate all the S_i 's at once, placed into a vector.
help cvx/norm
Disciplined convex programming information:
norm is convex, except when P<1, so an error will result if
these non-convex “norms” are used within CVX expressions. norm
is nonmonotonic, so its input must be affine.
help norms
norms Computation of multiple vector norms.
norms( X ) provides a means to compute the norms of multiple vectors
packed into a matrix or N-D array. This is useful for performing
max-of-norms or sum-of-norms calculations.All of the vector norms, including the false "-inf" norm, supported by NORM() have been implemented in the norms() command. norms(X,P) = sum(abs(X).^P).^(1/P) norms(X) = norms(X,2). norms(X,inf) = max(abs(X)). norms(X,-inf) = min(abs(X)). If X is a vector, these computations are completely identical to their NORM equivalents. If X is a matrix, a row vector is returned of the norms of each column of X. If X is an N-D matrix, the norms are computed along the first non-singleton dimension. norms( X, [], DIM ) or norms( X, 2, DIM ) computes Euclidean norms along the dimension DIM. norms( X, P, DIM ) computes its norms along the dimension DIM. Disciplined convex programming information: norms is convex, except when P<1, so an error will result if these non-convex "norms" are used within CVX expressions. norms is nonmonotonic, so its input must be affine.
Thanks for your help!
I want to express the distance S_1<S_2, and S_1<3, but the problem of {convex} <= {convex} arises.
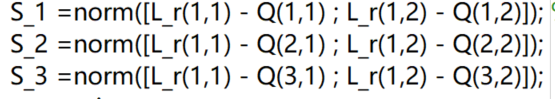
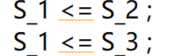
Those are non-convex constraints.
How to convert this non-convex constraint into a convex constraint
Have you read the link?
Non-convex optimization solvers (available under YALMIP, but not under CVX) exist because some optimization problems are non-convex.
Do you mean to use YALMIP this to solve this optimization problem? Do I need to put all my problems in YALMIP to use it?
If those are the constraints you need, then you can try YALMIP (you will need to use sqrtm instead of norm for the non-convex usage).
ok, thanks for your suggestion