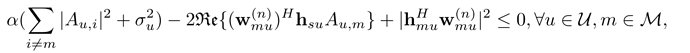How to solve the DCP error. Disciplined convex programming error: Invalid quadratic form(s): not a square

Nonconvex
1

> Disciplined convex programming error: Invalid quadratic form(s): not a square.

                    cvx_begin sdp quiet
                    variable alpha1 nonnegative
                    variable A(1,U) complex
                    variable B nonnegative
                    minimize rho/2*pow_pos(abs(A(1,u)-H(:,u)'*w1(:,u)+g(1,u)),2)+rho/2*pow_pos(abs(alpha1-delta1+f),2)
                    subject to
                            for u=1:U
                                A(1,u)==0;
                                B>=sum(pow_pos(abs(A),2));
                                gamma*(B+sigma)-2*real(w1(:,u)'*H(:,u).*A(1,u))+pow_pos(abs(H(:,u)'*w1(:,u)),2)<=0; 
                                alpha1*(B+sigma)-2*real(w1(:,u)'*H(:,u).*A(1,u))+pow_pos(abs(H(:,u)'*w1(:,u)),2)<=0; 
                            end
                    cvx_end
2

alpha1*(B+sigma) has a non-convex multiplication of variables alpha and B`. Have you proven this is a convex constraint? I will assume it is not, unless shown otherwise.

3

1
11462×113 11.5 KB

This picture is the constraint condition of objective function.
The eigenvalue of the Hesse matrix of the objective function is greater than or equal to zero.
Therefore, I think it is a convex constraint.
I’m not familiar enough with CVX to get it to work correctly.
How do I express this constraint condition?
Thank U so much.

4

You mention eigenvalue of Hessian of objective. Then you say convex constraint. You need to prove the constraint is convex. Perhaps \alpha is not supposed to be an optimization (CVX) variable?