Recently have been reading an article where I need to solve for a bivariate LMI. i have not been able to get the right answer, hopefully this can help me. Article name: From Noisy Data to Feedback Controllers:Nonconservative Design via a Matrix S-Lemma.
clear, clc;
% oo=1;
% EE=cell(100,100);
% cc=zeros(100,100);
% while(1)
%状态空间
A = [0.850 -0.038 -0.380;
0.735 0.815 1.594;
-0.664 0.697 -0.064];
B = [1.431 0.705;
1.620 -1.129;
0.913 0.369];
u = randn(2,20);
x0 = randn(3, 1);
%% 生成噪音
n = 3; % 噪声向量的长度
num_samples = 100; % 要生成的噪声向量数量
desired_norm_square = 0.5; %限制范数界
scaled_noises = zeros(n, num_samples);
for i = 1:num_samples
noise = randn(n, 1); % 生成高斯分布的随机噪声
while norm(noise, 2)^2 > desired_norm_square
noise = randn(n, 1); % 如果范数平方超过了阈值,重新生成噪声
end
scaled_noises(:, i) = noise;
end
% 从生成的噪声中随机抽取20列
num_selected = 20;
selected_indices = randperm(num_samples, num_selected);
w= scaled_noises(:, selected_indices);
%% 生成响应
t=20;x=[];x(:,1)=x0;
for i=1:t
x(:,i+1)=Ax(:,i)+Bu(:,i)+w(:,i);
end
x_i0=x(:,1:20);
x_i1=x(:,2:21);
U_i=u;
%% 求解LMI
%定义给定矩阵
I_3=eye(3);
I_0=zeros(3,3);
I_01=zeros(2,3);
I_02=zeros(1,20);
I_03=zeros(3,20);
I_04=zeros(20,3);
I_05=zeros(3,2);
I_06=zeros(2,3);
I_07=zeros(2,2);
a=randn;
b=randn;
fai_11=t0.5eye(3);
fai_22=-eye(20);
%% 定义N
A1=[I_3,x_i1;I_0,-x_i0;I_01,-U_i;I_0,I_03];
A2=[fai_11 I_03;I_04 fai_22];
N=aA1A2A1’;
[F2,G2]=eig(N);
G2;
N11=N(1:3,1:3);
N12=N(1:3,4:6);
N13=N(1:3,7:8);
N14=N(1:3,9:11);
N21=N(4:6,1:3);
N22=N(4:6,4:6);
N23=N(4:6,7:8);
N24=N(4:6,9:11);
N31=N(7:8,1:3);
N32=N(7:8,4:6);
N33=N(7:8,7:8);
N34=N(7:8,9:11);
N41=N(9:11,1:3);
N42=N(9:11,4:6);
N43=N(9:11,7:8);
N44=N(9:11,9:11);
% n = 23; % 方阵的大小
% N1 = zeros(n);
% % 设置左上角为3x3单位阵
% N1(1:3, 1:3) = 200.5eye(3);
% % 设置右下角为3x3单位阵
% N1(n-2:n, n-2:n) = -eye(3);
% N=aA1N1A1’;
%% 定义决策变量
% %CVX工具箱
cvx_begin
cvx_solver sdpt3
variable P(3, 3) semidefinite
variable L(2, 3)
minimize trace(P)
subject to
% [P-(bI_3)-N11,I_0-N12,I_05-N13,I_0-N14;I_0-N21,-P-N22,-(L’)-N23,I_0-N24;I_06-N31,-L-N32,I_07-N33,L-N34; I_0-N41,I_0-N42,(L’)-N43,P-N44]==semidefinite(11);% 半正定约束
[[P-(bI_3),I_0,I_05,I_0;I_0,-P,-(L’),I_0;I_06,-L,I_07,L;I_01,I_0,(L’),P]-N]==semidefinite(11);% 半正定约束
cvx_end
%定义优化问题
k=Linv(P);
U=A+(Bk);
[F1,E]=eig(U);
E
% EE{oo,oo}=E;
% oo=oo+1;
% if oo==100
% break;
% end
% end
% for i=1:100
% if any(max(EE{i,i})>=1)
% cc(i,i)=1;
% end
% end
% a=sum(cc(:));
% disp(a);
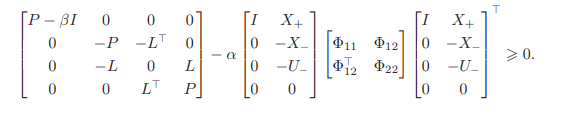
I don’t think you can expect forum readers to wade through a research paper, figure out what problem you are solving, understand the input data, understand why whatever solution you are getting is not the “right answer”, etc. Have you started by trying to duplicate an exact problem and input data shown in the paper, without resorting to your own random input data? Perhaps that would be a good start.
I have no idea why you describe this as a bivariate LMI problem. The dimension of the problem seems to exceed two, hence not bivariate.
Thank you very much for your reply. My reason for posting the paper was intended to be that I hoped that some readers had read it and might be able to provide me with help. The input data in the article is just randomly generated all may be different each time. I am not getting the correct results I suspect it is a problem with my program so I am hoping a reader can point out the error in the program. The bivariate LMI problem, which I simply understand as having two variables (P,L), is not clear from my theory. Thanks again for your reply!
