How to solve it in CVX

1

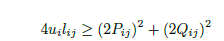
constrain
diag(real(S645))- real(loads([19, 35])) == diag(real(S645646))-diag(real(S632645)-Z632645*l632645)+diag(v645 * Cbus([19, 35],[19, 35]));

diag(imag(S645))- imag(loads([19, 35])) == diag(imag(S645646))-diag(imag(S632645)-Z632645*l632645)+diag(v645 * Cbus([19, 35],[19, 35]));

v632_abc([2, 3],[2, 3])*l645646>=real(S632645)*ctranspose(real(S632645))+imag(S632645)*ctranspose(imag(S632645));
Error using *
Disciplined convex programming error:
Only scalar quadratic forms can be specified in CVX
.
Error in SOCP_test (line 130)
v632_abc([2, 3],[2,3])*l645646>=real(S632645)*ctranspose(real(S632645))+imag(S632645)*ctranspose(imag(S632645));

Error in header (line 42)
[Voltage_profile, phasors] = SOCP_test(loads, Zbus, Cbus);

Could someone help me?

2

Presuming u and l are both > 0, the first constraint is a rotated 2nd order cone constraint:

I’ll let you deal with the subscripts as appropriate:

{[P;Q],u,l} == rotated_lorentz(2)

3

Thank you for your reply.
If P and Q are matrix case(P and Q are 22 matrix, u and l are also 22 matrix). This equation seems do not work.

The error is’ Matrix dimensions must agree’.
Could you please tell me how to solve it?

4

I was leaving you to deal with the subscripts, which you didn’t do. Now I’ll do it.

I think you may need a double for loop. Each constraint within the for loops would then have scalar P and Q

for i = 1:2
  for j = 1:2
    {[P(i,j);Q(i,j)],u(i),l(i,j)} == rotated_lorentz(2)
  end
end

I have corrected my previous post to eliminate the 2 's multiplying P and Q.

5

It really works
Thanks again for your reply.