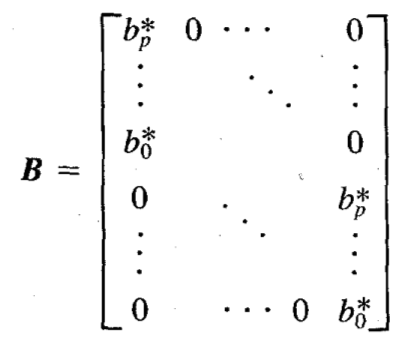
I have a vector b which constructs the matrix B:
When I define B as variable, I can’t compute the inverse of B’*B.
The convex problem is
Code is shown as following

Is there any method to find the inverse matrix? Thanks for your reply.
I have a vector b which constructs the matrix B:

When I define B as variable, I can’t compute the inverse of B’*B.
The convex problem is
Code is shown as following

Is there any method to find the inverse matrix? Thanks for your reply.
Is b the same as b* ? You haven’t shown us all the elements of B. I actually have no idea what the optimization problem is, because the listed optimization variables don’t explicitly appear in the objective, and you have not provided the information as to what their relationships are.
Without knowing the answers to all these, readers don’t even know what your problem is.
CVX does has matrrixfrac, But that requires the arguments be affine, which B'*B is not. But does B'*B reduce to something “nice” in terms of the optimization variables?
Please take it upon yourself to post clearly defined optimization problems on this forum. If you can’t do that because you don’t understand what the problem formulation in whatever paper or book you got the problem from is, you need to first understand yourself what the problem formulation is. And to have proven it is a convex optimization problem, per the FAQ link provided in this answer…
Please show us your convexity proof. Does convexity rely on the exact way B is constructed from b* ?