How to solve a constrained optimization problem of the form R<log(1+q2^2/q1^2)

Nonconvex
1

cvx_begin
variables sita_d(M,K) R_dd(K);

          maximize(sum(R_dd))
          subject to
           constr = uildConstraints(M,K,sita_d,erfa1,erfa2,R_dd,Gamma_uc,BETAA_uc)
        cvx_end

the following is constrain function
for m=1:M
y1(m)=(Gamma_uc(m,:)*sita_d(m,:)’);

end%
for k=1:K
q1(k)= (BETAA_uc(:,k)’*y1’)^2+noise_p^2; %concave
q2(k)=(Gamma_uc(:,k)’*sqrt(sita_d(:,k))) ;%concave
end
for k=1:K
c2 = [ R_dd(k)<=log(1+(q2(k))/(q1(k)))];
end
constr = [c2];

image
image945×559 14.2 KB

2

I believe this is non-convex.

3

log(1+x) is nondecreasing and concave, so if you wanna make this function concave, the argument must be concave.
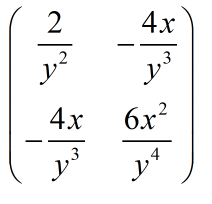Unfortunately, x^2/y^2 is non-concave, the Hessian is Snipaste_2020-11-07_14-40-43 .
And the determinant is image , this is negative.
By the way, we can’t derive a function concave from dividing a concave function by a concave function.

4

thank you,I realize that It is can,t be solve by CVX

5

thank you for replying me