How to represent this expression in CVX

1

123
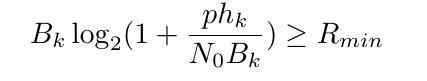
If there anyone know how to represent this expression in CVX？Only B_k is variable . Thanks advance！

2

-rel_entr(Bk,Bk+p*hk/N0)/log(2) >= Rmin

In general, x*log(1+y/x) can be formulated as -rel_entr(x,x+y) .presuming x is affine and y is concave (note that a numerical constant is concave).

3

Thanks for your help. I am very sorry that there is another problem :is that can achieve in CVX? Only B_k is variable too. And constraint of B_k is :0<=B_k <=B_max(a constant)
23

4

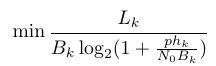
You can apply inv_pos, because it accepts a concave argument.

minimize(Lk*inv_pos(-rel_entr(Bk,Bk+p*hk/N0)/log(2)))
0 <= Bk <= B_max

help inv_pos

inv_pos Reciprocal of a positive quantity.
inv_pos(X) returns 1./X if X is positive, and +Inf otherwise.
X must be real.

 For matrices and N-D arrays, the function is applied to each element.

  Disciplined convex programming information:
      inv_pos is convex and nonincreasing; therefore, when used in CVX
      specifications, its argument must be concave (or affine).

You may benefit from a careful reading of the CVX Users’ Guide CVX Users’ Guide — CVX Users' Guide , as well as the Mosek Modeling Cookbook MOSEK Modeling Cookbook — MOSEK Modeling Cookbook 3.3.0

5

Hello @Mark_L_Stone , is this approach still applicable when you have A+N_0B_k in the log function instead of N_0B_k? A is constant. Thanks in advance.

6

Presuming A>= 0, the same basic idea can be used, with some extra complication: The expression after the lattermost = can be entered in CVX

x*log(1+y/(x+A)) = (x+A)*log(1+y/(x+A)) - A*log(1+y/(x+A))
= -rel_entr(x+A,x+A+y) - A*(rel_entr((x+A)/y,(x+A)/y+1) + rel_entr((x+A)/y+1,(x+A)/y))

If x and y are both variables, the decomposition in the first line does not result in a formulation which can be entered in CVX, although it is still mathematically correct. That is because A*log(1+y/(x+A) is neither convex nor concave jointly in x; and y, and therefore can;'t be reformulated for CVX, even though x*log(1+y/(x+A)) is jointly concave in x and y.

7

And of course you can apply inv_pos to this, if you want the reciprocal of this expression. And that would be convex.

1 Like