What exactly id your difficulty? That appears to be affine in a(n,m,k) which presumably would be declared as a 3D variable, and the sum is actually a triple summation over all 3 dimensions of a.
CVX reports error:
and my program is following: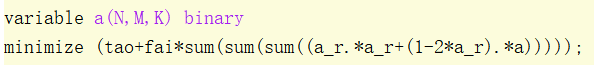
tao is also variable and fai is penalty constant
{invalid} is a CVX error message (usually?) means that there is NaN in the input data. If you are using SCA, that might be because the previous problem was not solved to optimality, due to being unbounded, infeasible, or solver having numerical difficulty, which causes CVX to populate variables with NaN. if you then use these as input data in the next iteration, you will get this error.
Are tao, fai, or a_r the optimal variable values from a previous iteration. In any event, just before the statement triggering the error message, print out their values and see if any of them are NaN.
for n=1:N
for m=1:M
for k=1:K
if (m==k)
a_r(n,m,k)=1;
else
a_r(n,m,k)=0;
end
end
end
end
fai=100;
cvx_solver Mosek
cvx_begin
variables T(N,M,3) q(2,N,M,3) e(N,M,3) x(N,M) y(N,M,K) tao;
variable a(N,M,K) binary
minimize (tao+fai*sum(sum(sum((a_r.a_r+(1-2a_r).*a)))));
tao is variable;fai and a_r is constant;I really use SCA method, but it
is the first iteration.
Why did you declare a as binary? Isn’t the point of this formulation that a is relaxed to be continuous
0 <= a <= 1 ?
I don’t see why you are getting the error. But you have not shown a complete reproducible problem starting from the beginning of a MATLAB session. You don’t show where you are iterating for SCA, etc. So it appears your error occurs due to something you are not showing us.
In any event, did you display the values of all the items in the objective function to see which, if any, are NaN?

clear all
clc
%%
fai=100;
N=4;
K=3;
M=K;
qb=[0,0]’;
qu=[1000,0]’;
s(:,1)=[200,700]’;
s(:,2)=[500 1000]’;
s(:,3)=[700 400]’;
delta0=410^5;
D=110^6;
B=510^6;
Pmax=0.1;
Emax=10;
Vmax=25;
epsilon=0.001;
H=100;
h=10;
gama0=10^7.3;
sigma=10^(-19);
%%
for n=1:N
for m=1:M
for k=1:K
if (m==k)
a(n,m,k)=1;
else
a(n,m,k)=0;
end
end
end
end
len=1000/(3N*M);
x=0;
for n=1:N
for m=1:K
for j=1:3
x=x+len;
q(:,n,m,j)=[x,0]’;
end
end
end
for n=1:N
for m=1:K
for j=1:3
T(n,m,j)=1;
end
end
end
%y(N,M,K)=0;
for n=1:N
for m=1:M
for k=1:K
y(n,m,k)=a(n,m,k)T(n,m,3);
end
end
end
for n=1:N
for m=1:M
for j=2:3
e(n,m,j)=1;
end
end
end
for n=1:N
for m=1:M
x(n,m)=(gama0e(n,m,3))/(norm(q(:,n,m,3)-qb)^2+(H-h)^2);
end
end
for n=1:N
for m=1:M
for k=1:K
c(n,m,k)=(sqrt(y(n,m,k)))/T(n,m,3);
end
end
end
%%
l=0;
delta=epsilon;
while delta>=epsilon
l=l+1;
a_r=a;
x_r=x;
for n=1:N
for m=1:M
for k=1:K
c(n,m,k)=(sqrt(y(n,m,k)))/T(n,m,3);
end
end
end
for n=1:N
for m=1:M
for k=1:K
if (m==k)
a_r(n,m,k)=1;
else
a_r(n,m,k)=0;
end
end
end
end
fai=100;
cvx_solver Mosek
cvx_begin
variables T(N,M,3) q(2,N,M,3) e(N,M,3) x(N,M) y(N,M,K) tao;
%variable a(N,M,K) binary
minimize (tao+fai*sum(sum(sum((a_r.a_r+(1-2a_r).*a)))));
subject to
%(24b)
for n=1:N
for m=1:M
(-rel_entr(T(n,m,3),T(n,m,3)+x(n,m))/log(2))>=D/B;
%T(n,m,3)*log2(1+(x(n,m)*inv_pos(T(n,m,3))))>=D/B;
end
end
%(24c)
for k=1:K
sum=0;
for n=1:N
for m=1:M
b=(y(n,m,k)+T(n,m,1)+T(n,m,2)+T(n,m,3));
sum=b+sum;
end
end
sum<=(N+1)*tao;
end
for n=1:N
for m=1:M
for k=1:K
a(n,m,k)>=0;
a(n,m,k)<=1;
end
end
end
%(24d)
for n=1:N
for m=1:M
for k=1:K
2*sqrt(y(n,m,k))*c(n,m,k)-T(n,m,3)*square_pos(c(n,m,k))>=a(n,m,k);
end
end
end
%(24e)
for n=1:N
for m=1:M
%(square_pos(norm(q(:,n,m,3)-qb))+(H-h)^2)inv_pos(gama0e(n,m,3))<=2/x_r(n,m)-x(n,m)/(x_r(n,m))^2;
quad_over_lin(q(:,n,m,3)-qb,gama0e(n,m,3))+(H-h)^2inv_pos(gama0*e(n,m,3))<=2/x_r(n,m)-x(n,m)/(x_r(n,m))^2;
end
end
%(15c)
for n=1:N
for m=1:M
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
sum2=0;
for k=1:K
w=a(n,m,k)s(:,k);
sum2=w+sum2;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
quad_over_lin(q(:,n,m,2)-sum2,e(n,m,2))+H^2inv_pos(e(n,m,2))<=delta0;
end
end
%(15d)
for n=1:N
for m=1:M
for i=2:3
0<=e(n,m,i);
e(n,m,i)<=Pmax*T(n,m,i);
end
end
end
%(15e)
sum1=0;
for n=1:N
for m=1:M
sum1=(e(n,m,2)+e(n,m,3))+sum1;
end
end
sum1<=Emax;
%(2)
norm(qu-q(:,1,1,1))<=T(1,1,1)*Vmax;
for n=1:N
for m=1:K
norm(q(:,n,m,1)-q(:,n,m,2))<=T(n,m,2)*Vmax;
norm(q(:,n,m,2)-q(:,n,m,3))<=T(n,m,3)*Vmax;
end
end
for n=1:N
for m=1:K-1
norm(q(:,n,m,3)-q(:,n,(m+1),1))<=T(n,(m+1),1)*Vmax;
end
end
for n=1:N-1
norm(q(:,n,K,3)-q(:,(n+1),1,1))<=T(n+1,1,1)*Vmax;
end
cvx_end
end
- List item
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 280
Cones : 132
Scalar variables : 641
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Eliminator - tries : 0 time : 0.00
Lin. dep. - tries : 0 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Optimizer terminated. Time: 0.08
Interior-point solution summary
Problem status : PRIMAL_INFEASIBLE
Solution status : PRIMAL_INFEASIBLE_CER
Dual. obj: 1.0000000000e+00 nrm: 7e+14 Viol. con: 0e+00 var: 1e-01 cones: 5e-09
Optimizer summary
Optimizer - time: 0.08
Interior-point - iterations : 0 time: 0.05
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Status: Infeasible
Optimal value (cvx_optval): +Inf
Thansks for your advice. Is there any question can we get from Mosek report?
The problem you feed into Mosek has bad numerical properties. Most likely the SCA algorithm relies on luck to some degree for it to work.
What @Erling wrote
plus
