![]()
Where X is an optimization variable, and X is a M×N matrix, X^H is the conjugate transpose of matrix X. Both A and B are given M×M complex matrix.
If anyone could give me some guidance, I would greatly appreciate it.
![]()
Where X is an optimization variable, and X is a M×N matrix, X^H is the conjugate transpose of matrix X. Both A and B are given M×M complex matrix.
If anyone could give me some guidance, I would greatly appreciate it.
If A = B, this can be reformulated as square_pos(norm(A*X,'fro')).
However, when A is different than B, it is not generally convex (or concave). Do you have a proof otherwise for your specific values of A and B ?
Firstly, thanks for your reply. And if the optimization variable here is R, the expression “trace(A×R×B^h)” is feasible, right?
If A and B are input data, trace(A*R*B')is affine. So it can be minimized or maximized in CVX, and used wherever CVX"s DCP rules allow affine expressions.
I presume by feasible, you mean “allowed by CVX”. Your use of 'feasible" to mean that may be confusing due to its meaning in optimization that an optimization problem has at least one point which satisfies all constraints.
Your understanding is accurate! What I want to express is “allowed by CVX”!
Hey Mark! I have annother question, if my optimization problem formulated as follows:
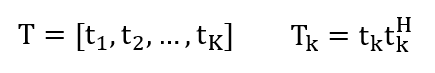
As you can see, all constraints are related to Tk, except for T in the objective function. So, my question is how to establish the relationship between Tk and T to make the objective function is only related to Tk? It troubles me so much! Do you have any advice? Thank you in advance!
Declared the t_k as variables and concatenate to form T.
Or perhaps more easily, declare T as a (matrix) variable, then extract the columns of T to use as t_k.
use square_pos(norm(x,'fro')) in place of trace(x*x')
So, the first constraint becomes:
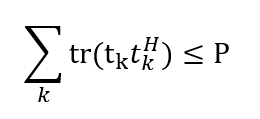
And denote the formulation trace(t_k×t_k^h) as square_pos(norm(t_k)). Is this right?
That is right.
…