I presume you mean u2= t*p2 and u3 = t*p3
As written, this is non-convex. In any event, the problem is unbounded (unless there are other constraints you haven’t shown), because p1, p2, p3 can go to infinity along with t, in order to retain feasibility.
If U1, u2, u3 were affine (or variables themselves), the constraint could be written as -rel_entr(t,u1+u2+u3)) >= 0 and would be allowed by CVX. But u1, u2, u3 are mot affine, and this constraint would therefore be rejected by CVX, whether or not in gp mode (gp mode would allow the multiplication of variables, but not what you subsequently did with them)…
In the future, please copy and past code using the Preformatted text icon, rather than posting an image of code.
Thank you, I was stupid and wrote the wrong formula.
But I have a question for you.
I’m doing a simulation on communication and I’ve simplified the formulas because they are too complicated.
One of the constraints takes the form of this equation tlog2(5p1+5p2+5p3+8)>=0.
Let u1=p1t,u2=p2t,u3=p3t. So the function is equivalent to tlog2(5u1/t+5u2/t+5u3/t+8), and has the same concavity as the function log2(5u1+5u2+5u3+8). By the perspective function theory we know that function tlog2(5u1/t+5u2/t+5u3/t+8) is convex with respect to t, u1,u2,u3.
Since it’s a standard convex constraint now, why doesn’t it work in CVX?
How should I write the code?
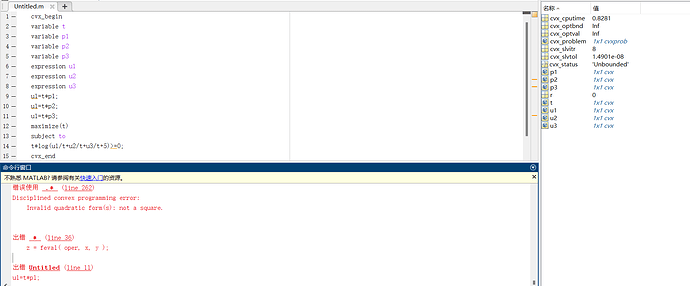
cvx_begin
variable t
variable p1
variable p2
variable p3
expression u1
expression u2
expression u3
expression d
u1=p1t;
u2=p2t;
u3=p3t;
maximize(t)
subject to
t(-rel_entr_quad(1,d))>=0;
d<=5u1/t+5u2/t+5*u1/t+8;
cvx_end
错误使用 .* (line 262)
Disciplined convex programming error:
Invalid quadratic form(s): not a square.
出错 * (line 36)
z = feval( oper, x, y );
出错 Untitled (line 10)
u1=p1*t;
Also, I wrote this objective function randomly, I just wanted to make cvx pass this constraint. Thank you very much, I hope you answer for me!
Leaving aside 8, the formulation and restrictions in the 3rd paragraph of my previous post still apply (if you divide everything by log(2)). I haven’t put in the effort to figure out how to deal with 8 (Edit: see my post after my next post for how to do that).
ylog(y/x) is a convex function, and this function has a specialized function expression inside CVX, namely rel_entr(y,x), and y log ( 1 + y/ x ) can be expressed inside CVX as rel_entr ( x + y , x ) + rel_entr ( x , x + y ).
alog(b/a+1)-alog(c/a+1) is the difference between two concave functions, how do I express this in CVX?
At this point, I am rather confused as to exactly what mathematical problem you are now trying to solve.
t*log2(5*u1/t+5*u2/t+5*u3/t+8) = -rel_entr(t,t+5/8*(u1+u2+u3))/log(2)+3*t
However, this requires u1, u2, u3 to be affine (or concave).
Thank you so much, you’ve helped me solve a difficult problem!