We want to minimize following function by using CVX:
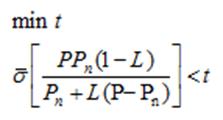
Where, “L” is matrix variable. Also, “P” and “Pn” are 2×2 matrix transfer function.
We want to minimize following function by using CVX:
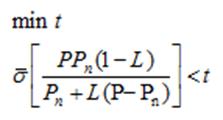
Where, “L” is matrix variable. Also, “P” and “Pn” are 2×2 matrix transfer function.
Have you proven the constraint is convex? It’s not obvious to me that it is. Actually, it’s not even obvious to me what the optimization problem specification even is. If L is a (2 by 2 ) matrix, what is 1 in 1 - L ? Maybe its supposed to be an I and is the identity matrix?
This problem will be marked non-convex until such time as you show that it is convex. I advise you to start by making a very clear statement on what everything is, including dimensions, and making clear what is input data and what are the optimization (decision) variables and make sure that ALL constraints are explicitly stated. Then determine whether that problem is convex. When you have done this, you may update your post.
Thank you very much for your immediate answer. Now, suppose that our system is single- input single- output (SISO).
If the right hand side was scalar function we could use “schur complement lemma” to transform into CVX format. But we have variables in both sides of inequality.
Is it possible to transform this problem in acceptable CVX format?
Have you read the link in my post? Have you proven convexity? “Almost” (but for this or that) doesn’t count in convexity analysis.