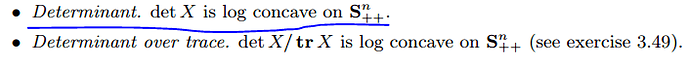Hi, my problem is as follows:
Can the complete formulation of the problem above be solved using CVX and how? Thanks a lot!
Is it convex? If so how have you proven it?
The matrix in the bracket is symmetric positive definite, so the objective is concave which makes a convex optimization problem. Is this a valid justification?
I’m afraid it is not.
The above is an example from the cvxbook.
In addition, the problem can be solved by the CVX if the term ![]() is removed from the objective.
is removed from the objective.
Of course I know these things. But (\mathop{\textrm{diag}}\alpha)-\alpha\alpha^T is a nonlinear expression. There is no guarantee that log-concavity will be preserved if you give the determinant function a nonlinear argument.
This is basic convex analysis. It is the reason why the composition rules are such a key part of the DCP ruleset, and why you must read and obey the FAQ if you intend to ask for help here.
Johan has reformulated this using Schur complement in a way which should be solvable in CVX. https://groups.google.com/forum/#!topic/yalmip/reuKgXVvQTE . Accordingly, I have removed the Nonconvex designation.
Fantastic! Thanks Mark.