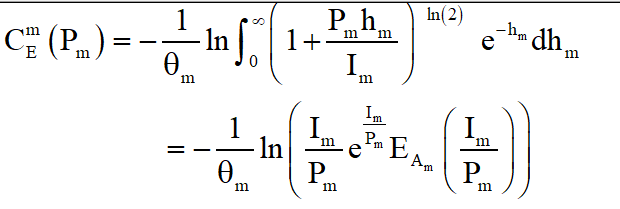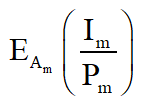How to handle log(x*exp(x))?

1

My optimization goal is
11

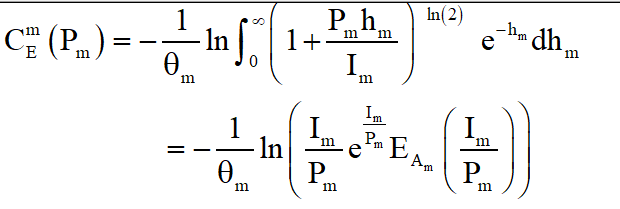
where EAm(x) is the exponential integral function of x.
I have proved that the optimization function is a convex function.

I use log_sum_exp to change the optimization goal, which is transformed as
(-1)/theta_m(i)*(log(Im(i)/pm(i).*exp(Im(i)/pm(i)))+log_sum_exp(Im(i)/pm(i)));

Then, I got
Disciplined convex programming error:
Cannot perform the operation: {positive constant} ./ {real affine}

I introduce a new variable t(i)=Im(i)/pm(i), then the optimization goal is transformed as
(-1)/theta_m(i)*(log(t(i).*exp(t(i)))+log_sum_exp(Im(i)/pm(i)));

Then, I got
Disciplined convex programming error:
Cannot perform the operation: {real affine} .* {log-affine}

When the optimization goal is transformed as
(-1)/theta_m(i)*(log(t(i))+t(i)+log_sum_exp(Im(i)/pm(i)));

Then, I got
Disciplined convex programming error:
Cannot perform the operation: {positive constant} ./ {real affine}

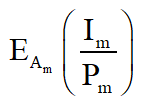
45%600D84PJFH%7BSZ%40BB2ETWTE
The expression above can be solved by CVX.

Is there any transformed function which can be used to handle ln(x*exp(x))?

2

log(x*exp(x)) = log(x) + x, which is concave.

2 Likes
3

Thank you. I forgot that… Can the expression that log(1/x*exp(1/x)) be solved by CVX ? Is there any transformed function?

4

I got the error as follows:
Disciplined convex programming error:
Cannot perform the operation: {positive constant} ./ {real affine}

5

If x > 0, then log(1/x*exp(1/x)) is convex and can be handled as
-log(x) + inv_pos(x)

6

Thanks for your help. log_sum_exp(x) is convex. But in this model, I need to use log_sum_exp(1/x). Then, I use a new variable t and add a new constraint t=1/x.
I got

Disciplined convex programming error:
Cannot perform the operation: {positive constant} ./ {real affine}

I got the convexity of the objective function by obtaining its second derivative.

\begin{array}{l} {\rm{ = }} - \frac{1}{{{\theta _m}}}\left( {\ln \left( {\frac{{{I_m}}}{{{P_m}}}{e^{\frac{{{I_m}}}{{{P_m}}}}}} \right){\rm{ + }}\ln \left( {{E_{{A_m}}}\left( {\frac{{{I_m}}}{{{P_m}}}} \right)} \right)} \right) \\ = - \frac{1}{{{\theta _m}}}\left( { - {\rm{log}}\left( {\rm{x}} \right){\rm{ }} + {\rm{ inv}}\_{\rm{pos}}\left( {\rm{x}} \right) + {\rm{log\_sum\_exp(}}\frac{{{I_m}}}{{{P_m}}}{\rm{)}}} \right) \\ \end{array}

The first term can be solved by CVX. But the second term can not. Is there any way to solve this problem?

7

help log_sum_exp

log_sum_exp log(sum(exp(x))).
log_sum_exp(X) = LOG(SUM(EXP(X)).

When used in a CVX model, log_sum_exp(X) causes CVX's successive
approximation method to be invoked, producing results exact to within
the tolerance of the solver. This is in contrast to LOGSUMEXP_SDP,
which uses a single SDP-representable global approximation.

If X is a matrix, LOGSUMEXP_SDP(X) will perform its computations
along each column of X. If X is an N-D array, LOGSUMEXP_SDP(X)
will perform its computations along the first dimension of size
other than 1. LOGSUMEXP_SDP(X,DIM) will perform its computations
along dimension DIM.

Disciplined convex programming information:
    log_sum_exp(X) is convex and nondecreasing in X; therefore, X
    must be convex (or affine).

help inv_pos

inv_pos Reciprocal of a positive quantity.
inv_pos(X) returns 1./X if X is positive, and +Inf otherwise.
X must be real.

 For matrices and N-D arrays, the function is applied to each element.

  Disciplined convex programming information:
      inv_pos is convex and nonincreasing; therefore, when used in CVX
      specifications, its argument must be concave (or affine).

Therefore, for vector x, log_sum_exp(1./x)) can be handled as
log_sum_exp(inv_pos(x))

I recommend you carefully read the entirety of the CVX Users’ Guide http://cvxr.com/cvx/doc/

8

Thank you for your help. I just started learning to use CVX. Then I will carefully read the CVX Users’ Guide. Thank you.