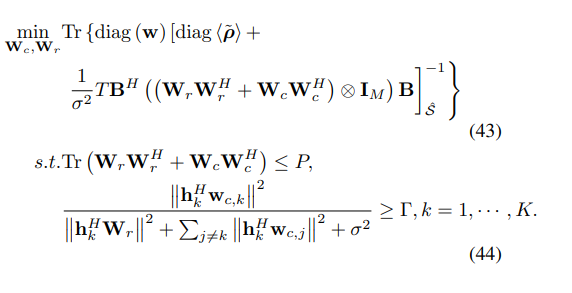My original problem, I use SDR method by replacing wrwr^H=Wr,wcwc^H=Wc. Since cvx doesn’t contain the operation of doing matrix inverse. So i cannot take the certain element of MSE^(-1). Instead, I change the weight matrix by replenishing the unwanted location with 0. But trace_inv operator is likely of no ability to solve trace_inv(w_diag*MSE) for sparse w_diag (of course i take the w_diag inverse in advance for restore). is there any other methods for solving this problem. i’m sure the problem is convex.
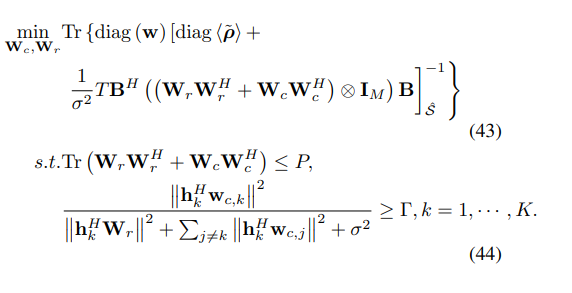
where 
First step for you: Have you proven this is a convex optimization problem?
Per the link, “being sure” it is convex is insufficient. If I had a nickel for every time a poster on this forum was sure their problem was convex, but it really wasn’t, I wouldn’t be rich, but I would have several dollars. If you are actually using some type of algorithm which solves a sequence of convex optimization problems in order to solve a non-convex optimization problem, you need to clearly state what those convex optimization problems are.
The first constraint can be rewritten as
square_pos(norm(Wr,'fro')) + square_pos(norm(Wc,'fro')) <= P
if wc were input data, the second constraint could be handled by multiplying through the LHS denominator, i.e, moving the denominator to the RHS. But apparently wc is not input data?
Wc is the variable which i want to reach. sorry for not giving enough evidence of convexity of the problem. for replacing wrwr^H=Wr,wcwc^H=Wc, So it can be a linear function of Wr and Wc? considering wr and wc is vector with dimension M*1, so Wr and Wc are hermitian semidefinite? thus from where i stand, i think the inverse of the whole matrix is positive semidefinite. But i donnot know how to use efficient methods to reduce the complexity of calculating the inverse, since all that is needed is the corresponding elements whose position lies in the support set.
The argument of trace_inv must be affine. In your case, the argument wouldn’t even be affine in Wr or Wc, let alone in wc.
You have failed to show this problem is convex. Please re-read the link in my previous post. I will assume the problem is not convex unless you prove otherwise.