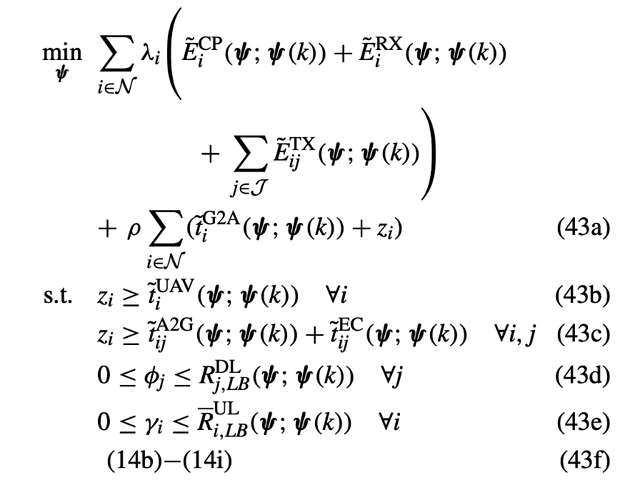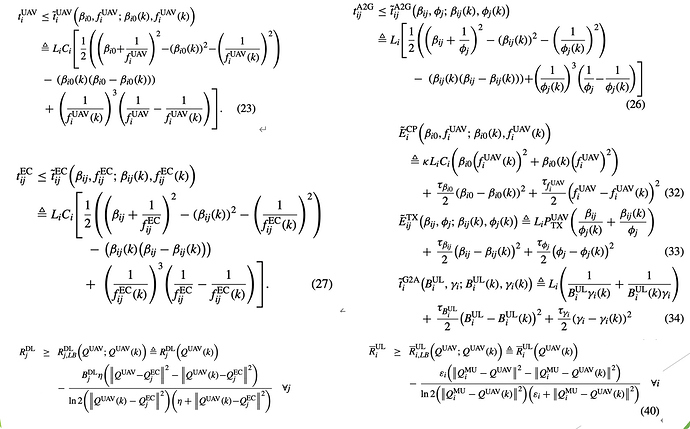I try to reproduce a paper which used SCA(successive convex approximation) algorithm to solved a jointly optimizing UAV position, communication and computing resource allocation, and task splitting decisions problem. But after I imitate their mathematical formulas I can not get the number which the paper solved and the number is too large(The optimal solution obtained by the first iteration is not on the same level as the final optimal solution in the article
), I‘m sure that the value shrinkage in my formula was in the range, so I decided to check my code right or not, then I have a question that when I use the function pow_pos(,2) in variables (in my code like f_UAV) to replace(.^2),the result are different between them, but I don’t know why, all my variables are positive, can you help me?
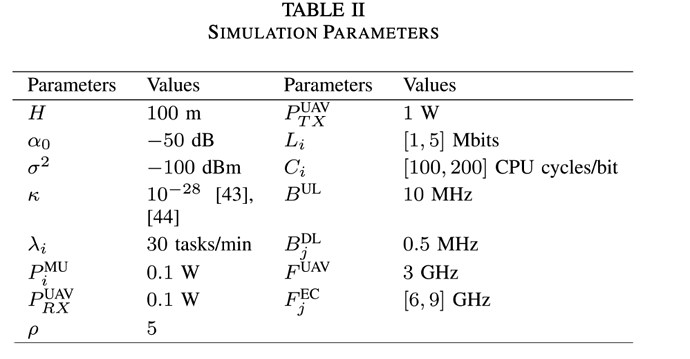
Here my mathematical formulas and code
**clc
clear all
close all
cvx_clear
k=1e-28;
L=[3;5;2;3;5;1;1;5;4;5].*1e6; %
C=[200;200;200;200;200;200;200;200;200;200];
lamda=[30;30;30;30;30;30;30;30;30;30];
rou=5;
tao_beitaij=1;
tao_faij=1;
tao_lamda=1;
tao_BUL=1;
tao_fUAV=1;
tao_beitai0=1;
P_UAVTX=1;
P_UAVRX=0.1;
P_MU=[0.1;0.1;0.1;0.1;0.1;0.1;0.1;0.1;0.1;0.1;];
theta=10^((-100/10)-3);
B_DL=[0.5 0.5 0.5 0.5].*1e6;
B_ULtotal=1e7;
F_UAV=3e9;
F_EC=[8 9 6 7].*1e9;
a0=10^((-50)/10);
beita_i00=[0.2;0.2;0.2;0.2;0.2;0.2;0.2;0.2;0.2;0.2];
f_UAV0=[0.1;0.1;0.1;0.1;0.1;0.1;0.1;0.1;0.1;0.1].*1e9;
beita_ij0=[0.2 0.2 0.2 0.2;0.2 0.2 0.2 0.2;0.2 0.2 0.2 0.2;0.2 0.2 0.2 0.2;…
0.2 0.2 0.2 0.2;0.2 0.2 0.2 0.2;0.2 0.2 0.2 0.2;0.2 0.2 0.2 0.2;0.2 0.2 0.2 0.2;0.2 0.2 0.2 0.2];
f_EC0=[0.1 0.1 0.1 0.1;0.1 0.1 0.1 0.1;0.1 0.1 0.1 0.1;…
0.1 0.1 0.1 0.1;0.1 0.1 0.1 0.1;0.1 0.1 0.1 0.1;…
0.1 0.1 0.1 0.1;0.1 0.1 0.1 0.1;0.1 0.1 0.1 0.1;0.1 0.1 0.1 0.1].*1e9;
langda0=[0.1;0.1;0.1;0.1;0.1;0.1;0.1;0.1;0.1;0.1];
fai_j0=[0.1 0.1 0.1 0.1];
B_UL0=[0.5;0.5;0.5;0.5;0.5;0.5;0.5;0.5;0.5;0.5].*1e6;
Q_UAVx0=5;
Q_UAVy0=7;
Q_UAV0=[Q_UAVx0,Q_UAVy0,100];
Q_EC=[0 0 0;1000 0 0;1000 1000 0;0 1000 0]
r =round( 0 + (500+500)*rand(1,20));
Q_MU=[r(1) r(2) 0;r(3) r(4) 0;r(5) r(6) 0;r(7) r(8) 0;r(9) r(10) 0;…
r(11) r(12) 0;r(13) r(14) 0;r(15) r(16) 0;r(17) r(18) 0;r(19) r(20) 0]
primal_obj_old=-inf;
for jjj=1:100
cvx_begin
cvx_solver mosek
variables beita_i0(10,1)
variables f_UAV(10,1)
variables beita_ij(10,4)
variables fai_j(1,4)
variables f_EC(10,4)
variables B_UL(10,1)
variables langda(10,1)
variables Q_UAVx Q_UAVy
variables z(10,1)
expression loc1(1,4)
loc1=;
for i=1:4
loc1=[loc1 pow_pos(norm([Q_UAVx Q_UAVy 100]-Q_EC(i,:)),2)];
end
expression loc2(1,4)
loc2=;
for i=1:4
loc2=[loc2 pow_pos(norm([Q_UAVx0 Q_UAVy0 100]-Q_EC(i,:)),2)];
end
expression loc3(10,1)
loc3=;
for i=1:10
loc3=[loc3;pow_pos(norm(Q_MU(i,:)-[Q_UAVx Q_UAVy 100]),2)];
end
expression loc4(10,1)
loc4=;
for i=1:10
loc4=[loc4;pow_pos(norm(Q_MU(i,:)-[Q_UAVx0 Q_UAVy0 100]),2)];
end
minimize (sum(lamda.*(((k.L.C.((beita_i0.(f_UAV0.^2))+beita_i00.*pow_pos(f_UAV,2)))+((tao_beitai0./2).pow_pos(beita_i0-beita_i00,2))+((tao_fUAV./2).pow_pos(f_UAV-f_UAV0,2)))…
+(P_UAVRX.((L.((1.*inv_pos(B_UL.*langda0))+(1.*inv_pos(B_UL0.*langda))))+((tao_BUL./2).*pow_pos(B_UL-B_UL0,2))+((tao_lamda./2).pow_pos(langda-langda0,2))))…
+sum((repmat(L,1,4).P_UAVTX.((beita_ij./repmat(fai_j0,10,1))+(beita_ij0.inv_pos(repmat(fai_j,10,1)))))+((tao_beitaij./2).(pow_pos(beita_ij-beita_ij0,2)))+repmat(((tao_faij./2).pow_pos(fai_j-fai_j0,2)),10,1),2)))…
+(rou.(sum(((L.((1.*inv_pos(B_UL.*langda0))+(1.*inv_pos(B_UL0.*langda))))+((tao_BUL./2).*pow_pos(B_UL-B_UL0,2))+((tao_lamda./2).*pow_pos(langda-langda0,2)))+z))))
subject to
z>=(L.*C.*((0.5.*(pow_pos((beita_i0+(1.*inv_pos(f_UAV))),2)-(beita_i00.^2)-(1./f_UAV0).^2))-(beita_i00... %?????
.*(beita_i0-beita_i00))+(pow_pos((1./f_UAV0),3).*((1.*inv_pos(f_UAV))-(1./f_UAV0)))));
repmat(z,1,4)>=(repmat(L,1,4).*(((0.5.*(pow_pos(beita_ij+repmat((1.*inv_pos(fai_j)),10,1),2)-pow_pos(beita_ij0,2)-repmat(pow_pos(1./fai_j0,2),10,1)))-...
(beita_ij0.*(beita_ij-beita_ij0))+(repmat(pow_p(1./fai_j0,3),10,1).*repmat((1.*inv_pos(fai_j))-(1./fai_j0),10,1)))))+...
(repmat(L,1,4).*repmat(C,1,4).*((0.5.*(pow_pos(beita_ij+(1.*inv_pos(f_EC)),2)-pow_pos(beita_ij0,2)-pow_pos(1./f_EC0,2)))...
-(beita_ij0.*(beita_ij-beita_ij0))+((pow_pos(1./f_EC0,3)).*((1.*inv_pos(f_EC))-(1./f_EC0)))));
0<=fai_j<=(B_DL.*log2(1+((a0./loc2).*P_UAVTX./theta))-...
((B_DL.*(a0.*P_UAVTX./theta).*(loc1-loc2))./...
(log(2).*loc2.*((a0.*P_UAVTX./theta)+loc2))));
0<=langda<=B_UL.*log2(1+((a0./loc4).*P_MU./theta))-((...
(a0.*P_MU./theta).*(loc3-loc4))./...
(log(2).*loc4.*((a0.*P_MU./theta)+loc4)));
sum(B_UL,2)<=B_ULtotal;
beita_i0+sum(beita_ij,2)==1;
sum(f_UAV)<=F_UAV;
sum(f_EC)<=F_EC;
0<=beita_ij<=1;
0<=beita_i0<=1;
B_UL>=0;
f_UAV>=0;
f_EC>=0;
0<=Q_UAVx<=1000;
0<=Q_UAVy<=1000;
cvx_end
beita_i00=beita_i00+(beita_i0-beita_i00)./jjj;
f_UAV0=f_UAV0+(f_UAV-f_UAV0)./jjj;
beita_ij0=beita_ij0+(beita_ij-beita_ij0)./jjj;
fai_j0=fai_j0+(fai_j-fai_j0)./jjj;
f_EC0=f_EC0+(f_EC-f_EC0)./jjj;
langda0=langda0+(langda-langda0)./jjj;
B_UL0=B_UL0+(B_UL-B_UL0)./jjj;
Q_UAV0=Q_UAV0+([Q_UAVx Q_UAVy 100]-Q_UAV0)./jjj;
primal_obj = cvx_optval;
cur_err= abs(primal_obj -primal_obj_old);
if primal_obj>primal_obj_old
primal_obj_old=primal_obj;
end
if cur_err<10^-2 %terminate condition
break
end
Q_UAV0
end
**
Here is the running result
Q_EC =
0 0 0
1000 0 0
1000 1000 0
0 1000 0
Q_MU =
789 368 0
206 87 0
772 206 0
388 552 0
229 642 0
484 152 0
782 101 0
294 237 0
531 91 0
405 105 0
Calling SDPT3 4.0: 1863 variables, 878 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.
num. of constraints = 878
dim. of sdp var = 812, num. of sdp blk = 406
dim. of socp var = 56, num. of socp blk = 14
dim. of linear var = 579
dim. of free var = 10 *** convert ublk to lblk
number of nearly dependent constraints = 10
To remove these constraints, re-run sqlp.m with OPTIONS.rmdepconstr = 1.
SDPT3: Infeasible path-following algorithms
version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
0|0.000|0.000|1.7e+04|2.4e+01|1.3e+23| 5.025889e+20 0.000000e+00| 0:0:00| spchol 2 3
1|0.010|0.000|1.6e+04|2.4e+01|1.4e+23| 6.159865e+20 -1.375841e+18| 0:0:00| spchol * 5 * 5
2|0.001|0.004|1.6e+04|2.4e+01|1.4e+23| 6.267425e+20 -1.547014e+18| 0:0:00| spchol * 5 * 5
3|0.028|0.001|1.6e+04|2.4e+01|1.5e+23| 8.558444e+20 -1.605570e+18| 0:0:00| spchol * 5 * 6
4|0.017|0.013|1.6e+04|2.4e+01|1.5e+23| 9.567931e+20 -2.111862e+18| 0:0:00| spchol * 5 * 6
5|0.068|0.010|1.5e+04|2.3e+01|1.5e+23| 1.318781e+21 -2.483743e+18| 0:0:01| spchol * 6 * 6
6|0.144|0.031|1.2e+04|2.3e+01|1.5e+23| 1.947238e+21 -3.653505e+18| 0:0:01| spchol * 6 * 7
7|0.269|0.066|9.1e+03|2.1e+01|1.6e+23| 2.838445e+21 -6.297933e+18| 0:0:01| spchol * 7 * 8
8|0.282|0.132|6.5e+03|1.8e+01|1.5e+23| 3.349461e+21 -1.183620e+19| 0:0:01| spchol * 8 * 8
9|0.528|0.157|3.1e+03|1.5e+01|1.4e+23| 3.644646e+21 -1.801620e+19| 0:0:01| spchol *10 *10
10|0.531|0.294|1.4e+03|1.1e+01|1.0e+23| 3.249913e+21 -3.004696e+19| 0:0:01| spchol *14 *13
11|0.460|0.212|7.8e+02|8.6e+00|8.2e+22| 2.936009e+21 -4.320327e+19| 0:0:01| spchol *19 *19
12|0.439|0.166|4.4e+02|7.2e+00|7.2e+22| 2.737001e+21 -5.925888e+19| 0:0:01| spchol
warning: symqmr failed: 0.3
switch to LU factor. splu 30 13
13|0.384|0.150|2.7e+02|6.1e+00|6.4e+22| 2.659816e+21 -7.899802e+19| 0:0:01| splu 30 16
14|0.443|0.170|1.5e+02|5.1e+00|5.6e+22| 2.517827e+21 -1.120309e+20| 0:0:01| splu 30 30
15|0.469|0.192|8.2e+01|4.1e+00|4.7e+22| 2.279828e+21 -1.508458e+20| 0:0:01| splu 30 ^ 8
16|0.294|0.202|5.8e+01|3.3e+00|3.9e+22| 2.109573e+21 -1.898251e+20| 0:0:01| splu 30 30
17|0.567|0.106|3.2e+01|2.9e+00|3.7e+22| 1.949513e+21 -2.167924e+20| 0:0:01| splu 14 ^29
18|0.141|0.118|2.8e+01|2.6e+00|3.6e+22| 2.091428e+21 -3.101573e+20| 0:0:01| splu 30 ^14
19|0.501|0.183|2.0e+01|2.1e+00|3.0e+22| 1.725468e+21 -3.292224e+20| 0:0:01| splu 30 ^ 8
20|0.694|0.235|7.8e+00|1.6e+00|2.4e+22| 1.245962e+21 -3.350959e+20| 0:0:01| splu 30 30
21|0.361|0.209|4.1e+01|1.3e+00|2.0e+22| 1.141141e+21 -3.540683e+20| 0:0:01| splu 30 ^28
22|0.379|0.125|2.3e+01|1.1e+00|1.9e+22| 1.105024e+21 -3.748136e+20| 0:0:01| splu 30 24
23|0.549|0.228|1.9e+01|8.6e-01|1.5e+22| 8.992556e+20 -3.760478e+20| 0:0:01| splu 28 ^ 8
24|0.432|0.182|1.8e+01|7.0e-01|1.4e+22| 8.109439e+20 -3.819716e+20| 0:0:01| splu 30 ^ 7
25|0.842|0.374|7.8e+00|4.4e-01|8.7e+21| 3.905579e+20 -3.052722e+20| 0:0:01| splu 30 ^ 6
26|0.503|0.180|8.0e+00|3.6e-01|7.6e+21| 3.876978e+20 -2.929489e+20| 0:0:01| splu 28 11
27|0.546|0.348|8.9e+00|2.4e-01|5.3e+21| 3.201538e+20 -2.414071e+20| 0:0:01| splu 30 9
28|0.649|0.196|4.1e+00|1.9e-01|4.4e+21| 2.961511e+20 -2.182403e+20| 0:0:01| splu *21 7
29|0.543|0.363|1.8e+00|1.2e-01|3.0e+21| 2.990942e+20 -1.753967e+20| 0:0:01| splu 22 9
30|0.683|0.220|3.9e+00|9.4e-02|2.3e+21| 2.213134e+20 -1.530681e+20| 0:0:01| splu 25 8
31|0.659|0.274|3.1e+00|6.8e-02|1.7e+21| 1.576966e+20 -1.264557e+20| 0:0:01| splu 27 8
32|0.715|0.252|3.7e+00|5.1e-02|1.3e+21| 1.059298e+20 -1.058788e+20| 0:0:01| splu 26 9
33|0.591|0.294|4.0e+00|3.6e-02|9.3e+20| 8.006943e+19 -8.452268e+19| 0:0:01| splu 26 8
34|0.808|0.273|5.2e+00|2.6e-02|6.7e+20| 4.821441e+19 -6.741043e+19| 0:0:01| splu 26 9
35|0.809|0.664|3.4e+00|8.8e-03|2.3e+20| 2.107302e+19 -2.537570e+19| 0:0:01| splu *18 5
36|0.868|0.319|1.4e+00|6.0e-03|1.5e+20| 9.162586e+18 -1.800489e+19| 0:0:02| splu *21 6
37|0.154|0.101|1.3e+00|5.4e-03|1.3e+20| 9.207745e+18 -1.678465e+19| 0:0:02| splu *15 4
38|0.341|0.131|9.2e-01|4.7e-03|1.2e+20| 9.184632e+18 -1.538585e+19| 0:0:02| splu *11 4
39|0.442|0.301|5.1e-01|3.3e-03|8.5e+19| 8.008734e+18 -1.196068e+19| 0:0:02| splu *23 5
40|0.749|0.288|6.6e-01|2.3e-03|5.9e+19| 4.402016e+18 -9.019957e+18| 0:0:02| splu 29 5
41|0.634|0.301|5.0e-01|1.6e-03|4.1e+19| 2.811765e+18 -6.639063e+18| 0:0:02| splu *25 4
42|0.432|0.143|3.6e-01|1.4e-03|3.6e+19| 2.533650e+18 -5.918467e+18| 0:0:02| splu *27 4
43|0.478|0.275|1.7e-01|1.0e-03|2.7e+19| 2.291061e+18 -4.703036e+18| 0:0:02| splu *21 4
44|0.596|0.187|2.6e-01|8.3e-04|2.3e+19| 1.857156e+18 -4.047724e+18| 0:0:02| splu *19 4
45|0.573|0.325|1.3e-01|5.6e-04|1.7e+19| 1.657265e+18 -3.109651e+18| 0:0:02| splu *18 4
46|0.740|0.220|1.3e-01|4.3e-04|1.3e+19| 1.246429e+18 -2.615403e+18| 0:0:02| splu *19 4
47|0.785|0.245|1.5e-01|3.3e-04|1.1e+19| 1.013819e+18 -2.153433e+18| 0:0:02| splu *20 4
48|1.000|0.268|1.5e-01|2.4e-04|8.3e+18| 7.506367e+17 -1.731449e+18| 0:0:02| splu *15 4
49|1.000|0.318|2.0e-01|1.6e-04|6.0e+18| 5.725661e+17 -1.319289e+18| 0:0:02| splu *21 4
50|1.000|0.323|2.6e-01|1.1e-04|4.3e+18| 4.130473e+17 -9.942905e+17| 0:0:02| splu 30 5
51|1.000|0.335|2.6e-01|7.4e-05|3.0e+18| 2.817193e+17 -7.328403e+17| 0:0:02| splu 30 4
52|1.000|0.302|2.5e-01|5.2e-05|2.2e+18| 2.158443e+17 -5.616259e+17| 0:0:02| splu 30 5
53|1.000|0.288|3.2e-01|3.7e-05|1.7e+18| 1.790304e+17 -4.403546e+17| 0:0:02| splu 30 4
54|1.000|0.306|4.8e-01|2.5e-05|1.3e+18| 1.396346e+17 -3.392532e+17| 0:0:02| splu 30 4
55|1.000|0.288|3.0e-01|1.8e-05|9.7e+17| 1.175420e+17 -2.683307e+17| 0:0:02| splu 30 4
56|1.000|0.306|3.8e-01|1.3e-05|7.3e+17| 9.269985e+16 -2.086533e+17| 0:0:02| splu 27 4
57|1.000|0.309|3.6e-01|8.7e-06|5.4e+17| 7.200974e+16 -1.616946e+17| 0:0:02| splu 30 4
58|1.000|0.295|5.8e-01|6.1e-06|4.1e+17| 5.929392e+16 -1.275931e+17| 0:0:02| splu 30 5
59|1.000|0.307|7.6e-01|4.3e-06|3.1e+17| 4.680194e+16 -9.956512e+16| 0:0:02| splu 25 5
60|1.000|0.331|6.2e-01|2.8e-06|2.1e+17| 3.324991e+16 -7.502507e+16| 0:0:02| splu *18 5
61|1.000|0.356|9.7e-01|1.8e-06|1.4e+17| 2.109045e+16 -5.393861e+16| 0:0:02| splu 25 4
62|1.000|0.391|5.3e-01|1.1e-06|8.6e+16| 1.157034e+16 -3.610402e+16| 0:0:02| splu 30 4
63|1.000|0.371|3.4e-01|7.0e-07|5.3e+16| 6.510262e+15 -2.445734e+16| 0:0:02| splu *12 4
64|1.000|0.367|4.4e-01|4.4e-07|3.3e+16| 3.711348e+15 -1.644853e+16| 0:0:02| splu *10 4
65|1.000|0.369|3.3e-01|2.8e-07|2.1e+16| 2.099792e+15 -1.091670e+16| 0:0:02| splu *10 4
66|1.000|0.377|2.5e-01|1.7e-07|1.3e+16| 1.151947e+15 -7.097388e+15| 0:0:02| splu * 9 4
67|1.000|0.385|2.2e-01|1.1e-07|7.7e+15| 6.118651e+14 -4.518512e+15| 0:0:02| splu * 9 3
68|1.000|0.388|2.7e-01|6.6e-08|4.7e+15| 3.221796e+14 -2.838329e+15| 0:0:02| splu * 8 3
69|1.000|0.388|1.4e-01|4.0e-08|2.8e+15| 1.730140e+14 -1.774844e+15| 0:0:02| splu * 8 3
70|1.000|0.384|1.3e-01|2.5e-08|1.7e+15| 9.680841e+13 -1.111216e+15| 0:0:02| splu * 8 3
71|1.000|0.380|1.4e-01|1.5e-08|1.1e+15| 5.732005e+13 -6.986651e+14| 0:0:02| splu * 8 3
72|1.000|0.374|1.6e-01|9.6e-09|6.5e+14| 3.612805e+13 -4.420458e+14| 0:0:02| splu * 8 3
73|1.000|0.366|6.9e-02|6.1e-09|4.0e+14| 2.398176e+13 -2.824673e+14| 0:0:02| splu * 8 3
74|1.000|0.348|6.1e-02|4.0e-09|2.8e+14| 1.654527e+13 -1.854650e+14| 0:0:02| splu 3 2
75|1.000|0.950|1.5e-05|2.0e-10|2.8e+13| 1.158651e+13 -1.129469e+13| 0:0:03| splu 2 2
76|1.000|0.951|3.6e-07|9.9e-12|1.2e+13| 7.312958e+12 -3.348098e+12| 0:0:03| splu 2 1
77|0.888|0.932|5.0e-08|8.5e-13|6.2e+12| 3.885587e+12 -1.809511e+12| 0:0:03| splu 2 1
78|1.000|0.944|5.9e-09|4.1e-13|2.3e+12| 1.458903e+12 -6.249753e+11| 0:0:03| splu 2 1
79|1.000|0.940|8.4e-10|5.7e-13|8.9e+11| 5.790933e+11 -2.404620e+11| 0:0:03| splu 2 1
80|0.972|0.953|1.3e-10|8.5e-13|1.7e+11| 1.020794e+11 -4.684638e+10| 0:0:03| splu 2 1
81|1.000|0.942|1.9e-10|1.3e-12|8.8e+10| 5.463944e+10 -2.598344e+10| 0:0:03| splu 2 1
82|1.000|0.958|1.0e-11|1.9e-12|2.4e+10| 9.637038e+09 -1.216459e+10| 0:0:03| splu 2 1
83|1.000|0.958|1.0e-12|2.1e-12|6.7e+09|-2.112530e+09 -8.159606e+09| 0:0:03| splu 2 1
84|1.000|0.956|5.2e-14|1.1e-12|2.1e+09|-5.206545e+09 -7.118510e+09| 0:0:03| splu 2 1
85|1.000|0.959|1.4e-14|1.0e-12|5.6e+08|-6.272374e+09 -6.765629e+09| 0:0:03| splu 1 1
86|1.000|0.964|8.6e-15|2.6e-13|9.1e+07|-6.585474e+09 -6.665834e+09| 0:0:03| splu 1 1
87|1.000|0.962|6.5e-15|6.0e-14|2.0e+07|-6.631173e+09 -6.650530e+09| 0:0:03| splu 2 1
88|1.000|0.960|6.0e-15|1.5e-14|4.8e+06|-6.640797e+09 -6.647500e+09| 0:0:03| splu 2 1
89|1.000|0.962|8.0e-15|3.1e-15|9.5e+05|-6.643300e+09 -6.646707e+09| 0:0:03| splu 2 1
90|1.000|0.957|5.2e-15|8.1e-16|2.6e+05|-6.643747e+09 -6.646567e+09| 0:0:03| splu 2 1
91|1.000|0.960|1.0e-14|2.0e-16|5.1e+04|-6.643882e+09 -6.646523e+09| 0:0:03| splu 2 1
92|0.967|0.955|1.3e-14|2.2e-16|1.3e+04|-6.643905e+09 -6.646515e+09| 0:0:03| splu 3 1
93|1.000|0.961|3.6e-14|2.3e-16|1.8e+03|-6.643913e+09 -6.646513e+09| 0:0:03| splu 11 ^12
stop: primal infeas has deteriorated too much, 2.0e-01
94|0.987|0.962|3.6e-14|2.3e-16|1.8e+03|-6.643913e+09 -6.646513e+09| 0:0:03|
number of iterations = 94
primal objective value = -6.64391289e+09
dual objective value = -6.64651288e+09
gap := trace(XZ) = 1.83e+03
relative gap = 1.37e-07
actual relative gap = 1.96e-04
rel. primal infeas (scaled problem) = 3.65e-14
rel. dual " " " = 2.31e-16
rel. primal infeas (unscaled problem) = 0.00e+00
rel. dual " " " = 0.00e+00
norm(X), norm(y), norm(Z) = 1.3e+10, 6.2e+20, 6.2e+20
norm(A), norm(b), norm(C) = 1.3e+04, 7.1e+09, 1.5e+10
Total CPU time (secs) = 2.94
CPU time per iteration = 0.03
termination code = -7
DIMACS: 1.7e-13 0.0e+00 4.0e-16 0.0e+00 2.0e-04 1.4e-07
Status: Inaccurate/Solved
Optimal value (cvx_optval): +6.64651e+09
Q_UAV0 =
90.2948 90.3252 100.0000
Calling SDPT3 4.0: 1863 variables, 878 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.
num. of constraints = 878
dim. of sdp var = 812, num. of sdp blk = 406
dim. of socp var = 56, num. of socp blk = 14
dim. of linear var = 579
dim. of free var = 10 *** convert ublk to lblk
number of nearly dependent constraints = 10
To remove these constraints, re-run sqlp.m with OPTIONS.rmdepconstr = 1.
SDPT3: Infeasible path-following algorithms
version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
0|0.000|0.000|5.0e+02|2.4e+01|5.4e+21| 1.991272e+19 0.000000e+00| 0:0:00| spchol 2 3
1|0.058|0.000|4.9e+02|2.4e+01|6.7e+21| 7.729482e+19 -2.071983e+16| 0:0:00| spchol * 4 * 5
2|0.001|0.023|4.9e+02|2.3e+01|6.5e+21| 7.738818e+19 -1.787391e+18| 0:0:00| spchol * 4 * 5
3|0.065|0.005|4.6e+02|2.3e+01|6.7e+21| 8.889765e+19 -2.168460e+18| 0:0:00| spchol * 5 * 5
4|0.070|0.029|4.3e+02|2.3e+01|6.7e+21| 9.963109e+19 -4.222247e+18| 0:0:00| spchol * 5 * 5
5|0.109|0.035|3.8e+02|2.2e+01|6.8e+21| 1.139689e+20 -6.596621e+18| 0:0:00| spchol * 5 * 5
6|0.173|0.053|3.1e+02|2.1e+01|6.8e+21| 1.319869e+20 -9.957124e+18| 0:0:00| spchol * 5 * 5
7|0.265|0.085|2.3e+02|1.9e+01|6.6e+21| 1.503848e+20 -1.475005e+19| 0:0:00| spchol * 4 * 4
8|0.460|0.155|1.2e+02|1.6e+01|5.9e+21| 1.542414e+20 -2.046502e+19| 0:0:00| spchol * 4 * 5
9|0.598|0.208|5.0e+01|1.3e+01|5.0e+21| 1.453100e+20 -2.626940e+19| 0:0:00| spchol * 5 * 5
10|0.504|0.227|2.5e+01|9.8e+00|4.1e+21| 1.354821e+20 -3.104644e+19| 0:0:00| spchol * 5 * 6
11|0.519|0.213|1.2e+01|7.7e+00|3.4e+21| 1.226921e+20 -3.306887e+19| 0:0:00| spchol * 6 * 6
12|0.529|0.208|5.6e+00|6.1e+00|2.8e+21| 1.089165e+20 -3.327434e+19| 0:0:00| spchol * 7 * 7
13|0.579|0.222|2.4e+00|4.8e+00|2.3e+21| 9.202875e+19 -3.171179e+19| 0:0:00| spchol * 9 * 9
14|0.599|0.237|1.1e+00|3.6e+00|1.8e+21| 7.465004e+19 -2.884172e+19| 0:0:00| spchol *12 *13
15|0.566|0.218|2.0e+00|2.8e+00|1.4e+21| 6.158946e+19 -2.612523e+19| 0:0:00| spchol *18 *21
16|0.415|0.142|5.0e+00|2.4e+00|1.3e+21| 6.038763e+19 -2.555195e+19| 0:0:00| spchol 28 27
17|0.613|0.260|1.8e+01|1.8e+00|1.0e+21| 4.739067e+19 -2.239379e+19| 0:0:00| spchol 29 30
18|0.418|0.221|1.6e+01|1.4e+00|8.2e+20| 4.092028e+19 -2.004388e+19| 0:0:01| spchol
warning: symqmr failed: 0.3
switch to LU factor. splu 30 ^17
19|0.534|0.188|2.6e+01|1.1e+00|6.8e+20| 3.256590e+19 -1.810235e+19| 0:0:01| splu 30 22
20|0.608|0.269|1.5e+01|8.3e-01|5.2e+20| 2.485001e+19 -1.551741e+19| 0:0:01| splu 29 ^ 6
21|0.349|0.184|1.8e+01|6.8e-01|4.4e+20| 2.300767e+19 -1.449969e+19| 0:0:01| splu 30 15
22|0.833|0.304|1.3e+01|4.7e-01|3.2e+20| 1.353783e+19 -1.179383e+19| 0:0:01| splu 30 ^22
23|0.658|0.225|3.9e+01|3.7e-01|2.6e+20| 1.248883e+19 -1.064158e+19| 0:0:01| splu 30 19
24|0.714|0.216|1.5e+01|2.9e-01|2.1e+20| 1.369408e+19 -9.820150e+18| 0:0:01| splu 30 30
25|0.612|0.254|2.2e+01|2.1e-01|1.6e+20| 1.259503e+19 -9.259809e+18| 0:0:01| splu 30 22
26|0.636|0.214|2.5e+01|1.7e-01|1.3e+20| 1.069479e+19 -8.709317e+18| 0:0:01| splu 30 22
27|0.655|0.339|3.5e+01|1.1e-01|8.8e+19| 7.254536e+18 -7.079327e+18| 0:0:01| splu 30 ^20
28|0.642|0.154|3.7e+01|9.4e-02|7.8e+19| 6.276246e+18 -6.727027e+18| 0:0:01| splu 30 11
29|0.884|0.841|1.3e+01|1.5e-02|1.4e+19| 2.003263e+18 -1.619381e+18| 0:0:01| splu 23 7
30|0.461|0.129|7.5e+00|1.3e-02|1.2e+19| 1.559916e+18 -1.500538e+18| 0:0:01| splu *21 6
31|0.417|0.270|4.9e+00|9.5e-03|9.0e+18| 1.321319e+18 -1.277567e+18| 0:0:01| splu 30 12
32|0.708|0.259|2.6e+01|7.1e-03|6.5e+18| 7.518227e+17 -1.031408e+18| 0:0:01| splu 30 9
33|0.621|0.281|1.4e+01|5.1e-03|4.7e+18| 4.970270e+17 -8.010590e+17| 0:0:01| splu 30 8
34|0.579|0.220|8.7e+00|4.0e-03|3.7e+18| 3.621357e+17 -6.642416e+17| 0:0:01| splu 30 7
35|0.505|0.172|5.0e+00|3.3e-03|3.2e+18| 3.122442e+17 -5.835789e+17| 0:0:01| splu 30 5
36|0.517|0.304|2.8e+00|2.3e-03|2.4e+18| 2.735691e+17 -4.621352e+17| 0:0:01| splu 30 7
37|0.694|0.196|3.2e+00|1.8e-03|2.0e+18| 2.122592e+17 -4.003505e+17| 0:0:01| splu 30 4
38|0.690|0.367|1.2e+00|1.2e-03|1.4e+18| 1.789471e+17 -3.020255e+17| 0:0:01| splu 30 6
39|0.920|0.251|1.9e+00|8.7e-04|1.1e+18| 1.206763e+17 -2.496049e+17| 0:0:01| splu 30 6
40|1.000|0.293|3.8e+00|6.1e-04|8.7e+17| 9.009266e+16 -1.979146e+17| 0:0:01| splu *22 5
41|1.000|0.354|4.1e+00|4.0e-04|6.0e+17| 5.725730e+16 -1.442639e+17| 0:0:01| splu *17 5
42|1.000|0.316|5.1e+00|2.7e-04|4.4e+17| 4.142333e+16 -1.093192e+17| 0:0:01| splu *24 5
43|1.000|0.270|4.1e+00|2.0e-04|3.6e+17| 3.763279e+16 -8.813638e+16| 0:0:01| splu 30 5
44|1.000|0.190|1.0e+01|1.6e-04|3.6e+17| 5.432949e+16 -8.021818e+16| 0:0:01| splu 30 5
45|1.000|0.592|2.4e+00|6.6e-05|1.7e+17| 2.786554e+16 -4.600493e+16| 0:0:01| splu 30 5
46|1.000|0.342|4.8e+00|4.3e-05|1.2e+17| 1.496494e+16 -3.414768e+16| 0:0:01| splu 30 5
47|1.000|0.369|3.9e+00|2.7e-05|7.8e+16| 8.596597e+15 -2.393588e+16| 0:0:01| splu 30 5
48|1.000|0.354|4.2e+00|1.8e-05|5.3e+16| 5.163083e+15 -1.688591e+16| 0:0:01| splu 30 5
49|1.000|0.353|3.5e+00|1.1e-05|3.5e+16| 3.171652e+15 -1.180109e+16| 0:0:01| splu *19 4
50|1.000|0.359|3.0e+00|7.3e-06|2.3e+16| 1.931806e+15 -8.101268e+15| 0:0:01| splu *11 4
51|1.000|0.364|2.7e+00|4.6e-06|1.5e+16| 1.159476e+15 -5.472439e+15| 0:0:01|
stop: lack of progress in primal infeas, homRd=Inf
number of iterations = 51
primal objective value = 2.78655377e+16
dual objective value = -4.60049295e+16
gap := trace(XZ) = 1.73e+17
relative gap = 2.34e+00
actual relative gap = 1.00e+00
rel. primal infeas (scaled problem) = 2.39e+00
rel. dual " " " = 6.56e-05
rel. primal infeas (unscaled problem) = 0.00e+00
rel. dual " " " = 0.00e+00
norm(X), norm(y), norm(Z) = 1.3e+15, 8.8e+19, 8.8e+19
norm(A), norm(b), norm(C) = 1.3e+03, 1.3e+08, 1.5e+10
Total CPU time (secs) = 1.48
CPU time per iteration = 0.03
termination code = -5
DIMACS: 1.3e+01 0.0e+00 1.1e-04 0.0e+00 1.0e+00 2.3e+00
Status: Failed
Optimal value (cvx_optval): NaN
Q_UAV0 =
291.4287 290.9253 100.0000
错误使用 + (第 83 行)
Disciplined convex programming error:
Illegal operation: {concave} + {convex}
出错 SCAlunwen (第 83 行)
+sum((repmat(L,1,4).P_UAVTX.((beita_ij./repmat(fai_j0,10,1))+(beita_ij0.inv_pos(repmat(fai_j,10,1)))))+((tao_beitaij./2).(pow_pos(beita_ij-beita_ij0,2)))+repmat(((tao_faij./2).*pow_pos(fai_j-fai_j0,2)),10,1),2)))…