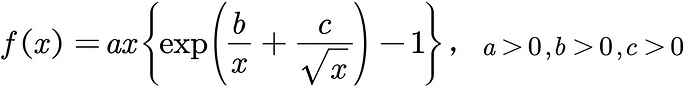Thanks in advance!
I have checked the function “x*(2^(1/x)-1)” is convex. I wonder how to express it in CVX to avoid the error “Cannot perform the operation: {real affine} .* {convex}”.
Are you @Wesen_Ning ? Your question looks very similar to How can cvx solve function like exp(x)*(exp(exp(-x))-1)? - #11 by Wesen_Ning . To minimize confusion, please stick with one username if possible.
Hello,could you tell me how to solve the functions like x*(exp(1/x) - 1) In detail
I provided there the solution
variables x z
{1,x,z} == exponential(1)Then x*(exp(1/x) - 1) can be formulated as z - x.
The exponential(1) constraint will constrain x > 0.
2^(1/x) can be rewritten as exp(log(2)/x)
so just change
{1,x,z} == exponential(1)
to
{log(2),x,z} == exponential(1)
Thanks for your help and sorry to confuse you, I’m a new user. Does the exponential(1) constraint require x to be a scalar? If x is a vector, what’s the difference in expression?
maybe CVX will deal with vector in an elementwise manner, just one by one
I can’t find this function exponential(1) in the CVX user’s guide. So, I’m so curious about the variables z and x means. Thanks!
It is documented as exp_cone in http://cvxr.com/cvx/doc/funcref.html#sets , but you need to use the syntax with exponential(1) rather than exp_cone.
If you have more than one of these constraints, specify them as individual scalar constraints inside a for loop.
Thanks, I find it in the CVX users’ guide.
Is there any method to represent this function, which is similar to the one above, but always displays real_ affine*log(convex).It’s really convex.
You posted this in a separate question?
Sorry, but reposting it here is very bad IMO because it is unrelated and wasting other peoples time.