How to express this sum of exponential perspective function constraint in CVX?

1

&\mathrm{C}{3}: \sum{i=1}^{N} y_{i} \cdot\left(\exp \left(\frac{x_{i}}{y_{i}}\right)-1\right) \leq \tau.
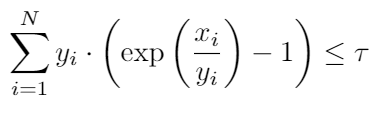
image
I’ve seen that we can use {x,y,z} == exponential(1) to represent y·exp(x/y) ≤ z. But when there is a summation of the perspective functions, how should we write it in CVX?

2 
variables x(N) y(N) z(N)
for i=1:N
  {x(i),y(i),z(i)} == exponential(1)
end
sum(z-y) <= tau
3

Thank you very much for responding. But I think at the end, it should be sum(z) <= tau.

4

I believe I had it correct. There is a y(i) times -1 term in the sum.

5

oh, yes, you are right, thank you very much!