How to express this function in CVX?

1

1
2

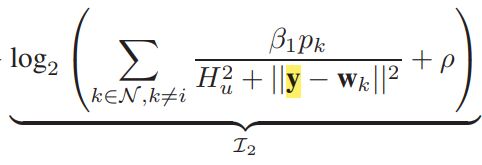
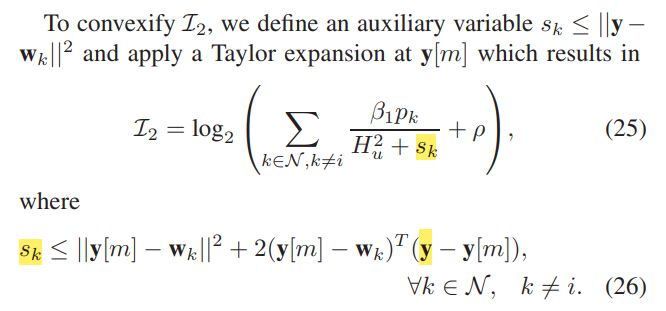
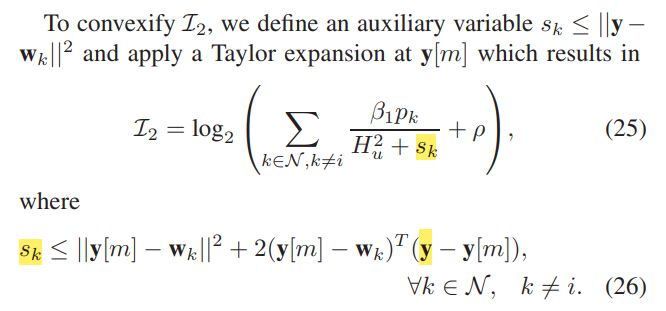
I have a less-than inequality constraint,where I2 is the left side,the right side is a constant.
How to express I2?and the yellow letter(y) is variable, y(2,1).

2

(25) looks doable. (26) does not look convex, per my interpretation.

You ought to be able to handle the LHS (i.e., (25)) using the first approach in section 5.2.7 Log-sum-inv of https://docs.mosek.com/modeling-cookbook/expo.html#exponential-cone by using CVX’s log_sum_exp for the ti >= … constraint, and also include the xi >= … constraint in that link as written.

x1 would be 1/rho, and the other xi’s would be something like (H^2+sk)/(beta1*pk) with indices suitably fixed up. And multiply the RHS by log(2) to account for log2.

Constraint (26) does NOT look convex to me. So I don’t see what the authors of that book or paper were doing.

3

Thank you for your reply.I will have a try.

4

hello, How did you solve this problem？

5

No, I am trying to use log_sum_inv

6

您好，请问您这个问题解决了吗？我们的问题很相似，方便的话我可以留个邮箱交流一下吗？

7

Thank you for your attention, I have not done this paper yet. You can reference these code, I hope it can help you.

    for i=1:N  
        v(n)=inv_pos( (H2+s(n))/(beta*p(n)) ); %calculat fraction v
    end
    for i=1:N       
        V(i)=sum(v([1:i-1 i+1:N]))+rol;  % sum+rol
    end
    for i=1:N 
        I2(i)=I2_f(i)+I2_df(i)*(V(i)-V_f(i)); % Taylor 
    end
    
    % I2_f(i)--- the feasible value of I2
    % V_f(i)---the feasible value of V,  V=sum+rol
    % I2_df(i)---the feasible value of 【derivative of log(V) in term of V】
8

Thank you very much for your prompt reply! Wishing you a pleasant day.

9

Well, I guess y is the only optimization variable in (26), and everything else, including w_k and y[m]` is input data. That would make (26) an affine constraint.

In the future, please state clearly what are optimization variables, and what is input data.