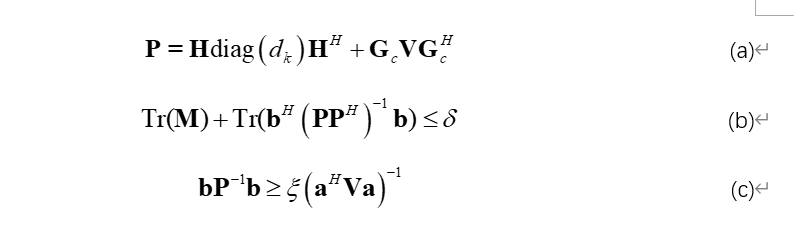As shown in the picture, could I express this equation using CVX? Or could I express this equation in an alternative way?
Thank you for your answer. There might be something wrong with the way I expressed my question.In fact, this is just a constraint issue in my optimization problem, such as trace(x^T·(P·P^T)^(-1)·x) ≤ δ, where δ is a constant, x is a constant vector, and P is an affine optimization variable. Could I express this form in CVX?
I was a little sloppy because I was looking at trace(X'*inv(P)*X) and showed the solution for that. Use my trace(Y) in place of trace(X'*inv(P)*X) and add the Schur Complement constraint I showed. That works provided trace(X'*inv(P)*X)appears in a convex manner in your optimization problem, such as minimizing it or being on LHS of <= .
But the last sentence of your first post and the constraint in the 2nd post, have inv(P*P') rather than inv(P). So what to do depends on whether or how P or P*P' appears in the rest of your optimization problem. If P never appears without an inverse, you can just use invP instead of P as your CVX variable and proceed accordingly. If P only appears in the form inv(P)*inv(P') you can make P your CVX variable and use the solution method in my old forum post I linked. if it always appears in product form, you can declare a “product variable” as the CVX variable, and then, after cvx)end, calculate matrixix square root or Choelsjy factor numerically of that variable.
So to get focused help, you should show us everywhere P or inv(P) appears in your model. Then we can figure out what to do, including even verifying the optimization problem is convex, which you should rigorously check yourself before posting.
thank you again! I will explain my thoughts to you.
As shown in the figure, equation (a) states that P is an affine function of the optimization variable d and the optimization variable V, with the rest being constants.
The occurrence of P is limited to only two places: one is the constraint for inv(PP') in (b), and the other is the use of inv(P) in (c). I have decided to handle this constraint (c) condition using SCA.
Therefore, only the trace(inv(PP')) in (b) cannot be expressed.
I edited my previous reply to trace(Y) from Y in the 2nd sentence.
Given the context you have now provided, your problem does appear to be non-convex, as you have apparently determined. SCA is an option for dealing with that, although no guarantees it will work well, or at all. Perhaps you’re already sort of doing this, but to move the odds of success more in your favor, given constraint (c), the penultimate paragraph of this post by Prof Stephen Boyd (his one and only post on this forum) might be the most pertinent, when suitably adapted to your problem. How to handle nonlinear equality constraints? - #5 by stephen_boyd for implementing the constraint in your 2nd post by SCA.