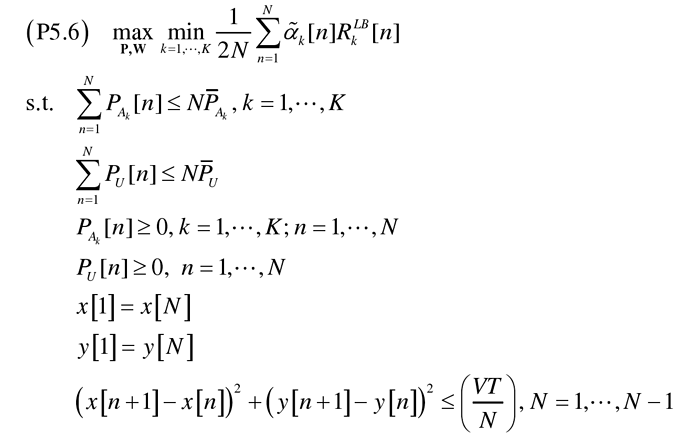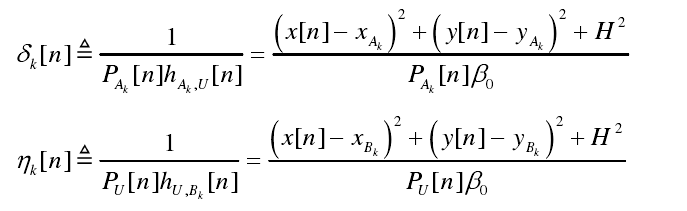
x[n],y[n],Pu[n],Pak[n] are variables to optimize.
for i = 1:K
for j=1:N
deltal(j,i) = prod_inv([inv_pos(((xl(j)-Ax(i)).^2+(yl(j)-Ay(i)).^2+h^2)), Pal(j,i)])/beta0;
yital(j,i) = quad_over_lin(norm([(xl(j)-Bx(i)),(yl(j)-By(i)),h],2),Pul(j))/beta0;
end
end
Both these two methods above can not solve my problem.
quad_over_lin, with the first argument being a 3 element vector, consisting of one element for each term being squared,should work.
help quad_over_lin
quad_over_lin Sum of squares over linear.
Z=quad_over_lin(X,Y), where X is a vector and Y is a scalar, is equal to
SUM(ABS(X).^2)./Y if Y is positive, and +Inf otherwise. Y must be real.If X is a matrix, quad_over_lin(X,Y) is a row vector containing the values of quad_over_lin applied to each column. If X is an N-D array, the operation is applied to the first non-singleton dimension of X. quad_over_lin(X,Y,DIM) takes the sum along the dimension DIM of X. A special value of DIM == 0 is accepted here, which is automatically replaced with DIM == NDIMS(X) + 1. This has the effect of eliminating the sum; thus quad_over_lin( X, Y, NDIMS(X) + 1 ) = ABS( X ).^2 ./ Y. In all cases, Y must be compatible in the same sense as ./ with the squared sum; that is, Y must be a scalar or the same size as SUM(ABS(X).^2,DIM). Disciplined convex programming information: quad_over_lin is convex, nonmontonic in X, and nonincreasing in Y. Thus when used with CVX expressions, X must be convex (or affine) and Y must be concave (or affine).
Thank you for helping me and my problem has been solved. I should just think in another point of view 
Excues me, May I ask why this problem is infeasible?
Here is my code:
cvx_begin
variable xl(N,1)
variable yl(N,1)
variable Pal(N,K)
variable Pul(N,1)
expression deltal(N,K)
expression yetal(N,K)
expression R(N,K)
for i = 1:K
for j=1:N
deltal(j,i) = quad_over_lin([(xl(j)-Ax(i)),(yl(j)-Ay(i)),h],Pal(j,i))/beta0;
yetal(j,i) = quad_over_lin([(xl(j)-Bx(i)),(yl(j)-By(i)),h],Pul(j))/beta0;
end
end
R = log2(1+gama)-C.(deltal-delta)-D.(yetal-yeta);
maximize min(diag(aR))
subject to
sum(Pal)<=NavPa;
sum(Pul)<=NavPu;
Pal>=0;
Pul>=0;
xl(1)==xl(N);
yl(1)==yl(N);
(arrxl).^2+(arryl).^2-(VT/N)^2<=0;
cvx_end
and here is the cvx information:
Calling SDPT3 4.0: 6304 variables, 1997 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.
num. of constraints = 1997
dim. of sdp var = 396, num. of sdp blk = 198
dim. of socp var = 5000, num. of socp blk = 1000
dim. of linear var = 710
number of dense column in A = 5
checkdepconstr: AAt is not pos. def.
SDPT3: Infeasible path-following algorithms
version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
0|0.000|0.000|1.3e+02|2.3e+01|1.3e+09| 2.232121e+07 0.000000e+00| 0:0:00| spchol
linsysolve: Schur complement matrix not positive definite
switch to LU factor. splu 1 1
1|0.962|0.962|4.8e+00|8.7e-01|5.5e+07| 5.580716e+06 -8.459186e+02| 0:0:00| splu 1 1
2|0.961|0.961|1.9e-01|3.4e-02|1.7e+06|-2.182570e+05 -5.415454e+02| 0:0:00| splu 2 1
3|0.637|0.581|7.0e-02|1.4e-02|7.1e+05|-4.122119e+05 -4.124946e+02| 0:0:00| splu 2 1
4|0.481|0.490|3.7e-02|7.3e-03|4.7e+05|-4.774647e+05 -2.880496e+02| 0:0:00| splu 2 1
5|0.278|0.456|2.7e-02|4.0e-03|4.3e+05|-5.165208e+05 -1.850162e+02| 0:0:01| splu 2 1
6|0.171|0.321|2.3e-02|2.8e-03|4.4e+05|-6.789654e+05 -1.325628e+02| 0:0:01| splu 2 1
7|0.288|0.337|1.7e-02|1.9e-03|4.2e+05|-8.918639e+05 -9.908716e+01| 0:0:01| splu 3 1
8|0.131|0.440|1.5e-02|1.1e-03|5.0e+05|-9.913634e+05 -5.744807e+01| 0:0:01| splu 3 1
9|0.291|0.198|1.1e-02|9.5e-04|5.1e+05|-1.273615e+06 -5.989365e+01| 0:0:01| splu 3 1
10|0.443|0.493|6.7e-03|5.0e-04|3.8e+05|-1.606352e+06 -2.645933e+00| 0:0:01| splu 4 1
11|0.414|0.408|4.6e-03|3.1e-04|3.9e+05|-1.631291e+06 1.447885e+01| 0:0:01| splu 5 1
12|0.436|0.476|3.4e-03|1.7e-04|3.5e+05|-1.772622e+06 1.668223e+01| 0:0:01| splu 14 2
13|0.293|0.450|2.9e-03|1.0e-04|4.1e+05|-1.883329e+06 1.621653e+01| 0:0:02| splu 30 3
14|0.469|0.419|2.8e-03|6.2e-05|3.5e+05|-1.834023e+06 -1.537244e+00| 0:0:02| splu 16 30
15|0.100|0.105|2.5e-03|5.9e-05|4.0e+05|-1.826429e+06 -5.753689e+00| 0:0:02| splu 30 ^ 7
16|0.003|0.004|2.4e-03|6.3e-05|4.4e+05|-1.819079e+06 -6.055287e+00| 0:0:02| splu 13 30
17|0.029|0.035|2.3e-03|6.6e-05|4.8e+05|-1.802461e+06 -9.141792e+00| 0:0:03| splu 24 ^ 7
18|0.041|0.028|2.4e-03|7.0e-05|5.3e+05|-1.772223e+06 -1.425465e+01| 0:0:03| splu 28 ^ 4
19|0.151|0.219|2.1e-03|6.1e-05|5.5e+05|-1.602685e+06 -3.604754e+01| 0:0:03| splu 30 ^ 8
20|0.285|0.439|2.6e-03|4.1e-05|5.5e+05|-1.201499e+06 -8.984426e+01| 0:0:03| splu 11 ^23
21|0.012|0.015|2.4e-03|4.8e-05|5.9e+05|-1.190067e+06 -8.975968e+01| 0:0:03| splu 14 ^29
22|0.030|0.039|2.4e-03|5.4e-05|6.2e+05|-1.156588e+06 -9.196781e+01| 0:0:04| splu 11 30
23|0.013|0.018|2.4e-03|6.2e-05|6.7e+05|-1.139939e+06 -9.433283e+01| 0:0:04| splu 30 ^17
24|0.036|0.027|2.0e-03|6.9e-05|7.2e+05|-1.100909e+06 -9.632542e+01| 0:0:04| splu 11 30
25|0.012|0.009|2.1e-03|7.9e-05|7.8e+05|-1.094467e+06 -9.831039e+01| 0:0:05| splu 30 30
26|0.004|0.008|2.1e-03|9.0e-05|8.5e+05|-1.089578e+06 -1.001736e+02| 0:0:05| splu 30 30
27|0.001|0.001|2.1e-03|1.0e-04|9.4e+05|-1.088946e+06 -1.005497e+02| 0:0:05| splu 30 ^14
28|0.004|0.004|1.8e-03|1.2e-04|1.0e+06|-1.089803e+06 -1.021536e+02| 0:0:05| splu 14 30
29|0.003|0.011|1.7e-03|1.3e-04|1.1e+06|-1.084699e+06 -1.075026e+02| 0:0:06| splu 30 ^23
30|0.003|0.010|1.6e-03|1.4e-04|1.2e+06|-1.079233e+06 -1.120753e+02| 0:0:06| splu 30 30
31|0.090|0.301|1.5e-03|1.2e-04|1.2e+06|-9.618745e+05 -2.332575e+02| 0:0:06|
sqlp stop: dual problem is suspected of being infeasible
number of iterations = 31
residual of dual infeasibility
certificate X = 1.04e-06
reldist to infeas. <= 2.18e-07
Total CPU time (secs) = 6.31
CPU time per iteration = 0.20
termination code = 2
DIMACS: 1.5e-03 0.0e+00 2.0e-03 0.0e+00 -1.0e+00 1.3e+00
Status: Infeasible
Optimal value (cvx_optval): -Inf
Except for section 1, the advice in https://yalmip.github.io/debugginginfeasible also applies to CVX.