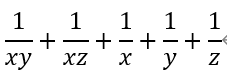
Hi, I want to use CVX to represent the formula in the figure above in the objective function (xyz is positive), what should I do, CVX does not seem to support multiplying two convex functions?
Assuming all variables must be nonnegative, then
implies
Therefore, you can use the geometric mean to build what you want.
Alternatively, you can use prod_inv, which implements @Erling’s geometric mean formulation “under the hood”.
The built-in function inv_pos is the same as prod_inv applied to a vector consisting of one element. It providew an additional option for the single variable terms.
Just to be clear, these formulations require x,y,z all > 0, although that need not be explicitly included in the CVX code, because that will be enforced by prod_inv, inv_pos, and geo_mean.
Actually, in my problem where the variable xyz has a range of (0,1), it seems that the above inequality does not hold.
Based on the values of the variables (they range from 0 to 1), I cannot introduce the t variable. As far as I know, I can use inv_pos (x) to represent 1/x, but I can’t represent 1/ (xy).
Range of )0,1) is fine. The only requirement for use of the offered solutions is nonnegatvity of all the variables.
I tried P (u) instead of 1/[X(u)Y(u)], Q (u) instead of 1/[X(u) Z(u)], and[X(u)*Y(u)*P (u) ]^(1/3)=> 1, [X(u)*Y(u)*Q (u) ]^(1/3) => 1 are the constraints. But the results are still wrong.
U=10;
cvx_begin quiet
% cvx_solver mosek
variables X(U) Y(U) Z(U) P(U) Q(U);
Obj = 0;
for u =1:U
Obj = Obj + P(u)+Q(u)+inv_pos(X(u))+inv_pos(Y(u))+inv_pos(Z(u));
end
minimize Obj;
subject to
for u = 1:U
0 < X(u)<=1;
end
for u = 1:U
0 < Y(u)<=1;
end
for u = 1:U
0 < Z(u)<=1;
end
for u = 1:U
1<= X(u)^(1/3)*Y(u)^(1/3)*P(u)^(1/3);
end
for u = 1:U
1<= X(u)^(1/3)*Y(u)^(1/3)*Q(u)^(1/3);
end
cvx_end

Use one of the formulations provided (geometric_mean or prod_inv). There will be no multiplications in the arguments of either formulation.