How to express a generalized inequality contained in the constraint in matlab? Can I use “>=” directly?
You need to be more specific as to what this “generalized inequality” is. “Generalized” inequality. has several different meanings.
If you are referring to a cone "inequality as in section 5.9 of https://web.stanford.edu/~boyd/cvxbook/ , CVX can handle it for the cone type it supports (SOCP, exponential, Linear SDP (a.k.a. LMI)).
Thanks for your reply! This is my convex optimization problem:
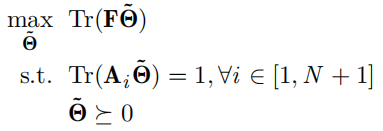
Where ![]()
![]() is a complex matrix, and its value on the primary diagonal is real number.
is a complex matrix, and its value on the primary diagonal is real number. ![]()
![]() is a symmetric positive semidefinite matrix.
is a symmetric positive semidefinite matrix. ![]() is an interesting matrix with only one element of value 1, and the element exists on the (i, i)-th coordinate of
is an interesting matrix with only one element of value 1, and the element exists on the (i, i)-th coordinate of ![]() .
.
The first problem is: I want to express the constraint"![]() " in matlab, so I define the variable in the way: “variable theta_relax(N,N) hermitian semidefinite;” is this right?
" in matlab, so I define the variable in the way: “variable theta_relax(N,N) hermitian semidefinite;” is this right?
The second problem is: the objective function “![]() ” is a complex number, when I run the code, matlab will say “Expressions in objective functions must be real.” So I redefine the objective function in matlab in the way “maximize (real(trace(F * theta_relax)))” (I directly used the real function to make the value of the original objective function a real number). Is this right? will the results of the original optimization goals change?
” is a complex number, when I run the code, matlab will say “Expressions in objective functions must be real.” So I redefine the objective function in matlab in the way “maximize (real(trace(F * theta_relax)))” (I directly used the real function to make the value of the original objective function a real number). Is this right? will the results of the original optimization goals change?
Here is my code:
N = N+1;
cvx_begin sdp quiet
variable theta_relax(N,N) hermitian semidefinite;
maximize (real(trace(F * theta_relax)))
subject to
for p = 1:N
A_p = A(1:N,1:N,p);
trace(A_p * theta_relax) == 1;
end
cvx_end
Your code relating to A looks flaky. Put the A_i in a N+1 by N+1 by +11 3D array, with the last dimension being for the index i, and the first two dimensions containing A_i. In general, for this data structure, the length of the last dimension need not be the same as the first two.
As for the trace evaluating to complex, there are two possibilities.
- It would be real if evaluated in exact arithmetic, but when evaluated in double precision, there is a roundoff level imaginary term. In this case, you can apply real, and everything should be fine.
- The objective does not evaluate to real, even inexact arithmetic. In this situation, you are the “author” of the model (in the sens you are the one who took the problem from a paper, book, your advisor’s notes, or whatever), so it is incumbent to figure out what the objective should be to address whatever real-world problem (such as getting a Ph.D. or tenure) the model’s solution is intended to address.
If both matrices which are being multiplied in the trace are hermitian semidefinite, then the trace evaluates to real in exact arithmetic, as you can see by factorizing the matrices, permute per the cyclic permutation invariance of trace, then converting to a square Frobenius non, which evaluates to a real scalar. So that would place you in situation 1.However, your description does not suggest F is hermitian semidefinite; so it is not apparent to me that the trace is real. So you’re in situation 2, and you are the expert in the model, or at least you should become one, so you need to figure out what the model is supposed to be. it’s not my model, and I have no context, so I have no idea. And even if I had the context, it would be off-topic for me to explain your model to you; that is your responsibility, and is a prerequisite to entering it in CVx and solving it.
Thank you for your reply, which has given me a lot of inspiration! I will continue to work hard.
I wish you a happy life!