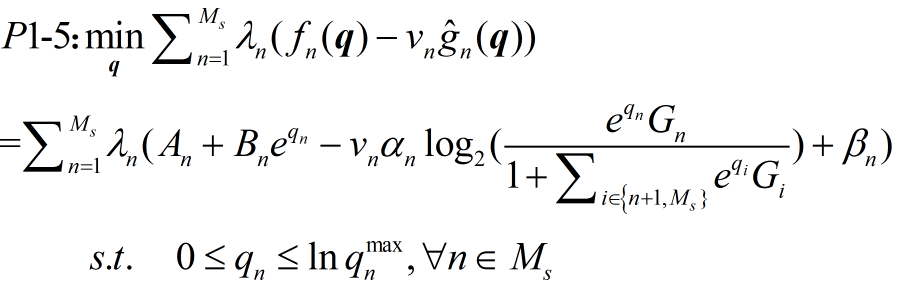Dear all:
I’m trying to solve the following covex problem using CVXQUAD, but I don’t know how to
modify the log(expression) and the exp(expression);
The objective optimization formulation is
clc
temp=2;
lambda=[0.234650415022566,0.141198274890993];
A=[1.70249073528940,1.50711646801602];
B=[323.300404329147,1567.27414459861];
alpha=[0.947866980725096,0.992620388932429];
beta=[0.295389685752478,0.0628713206907969];
v=[0.458378689078998,0.267368274162247];
gain=[3173934.01464403,545508.760914290];
MaxPowerOfUE=0.1995;
cvx_begin
variable x(temp)
dual variables y
minimize lambda(1)*(A(1)+B(1)*exp(x(1))-v(1)*(alpha(1)/log(2)*log(gain(1)*exp(x(1))/(1+gain(2)*exp(x(2))))+beta(1)))+...
lambda(2)*(A(2)+B(2)*exp(x(2))-v(2)*(alpha(2)/log(2)*log(gain(2)*exp(x(2)))+beta(2)))
subject to
y : x<=log(MaxPowerOfUE);
cvx_end
Look at he Logistic regression equations under Figure 7.1 on p. 356 of Boyd and Vandenberghe “Convex Optimization” http://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf . And see the code at http://web.cvxr.com/cvx/examples/cvxbook/Ch07_statistical_estim/html/logistics.html .
That should allow you to use log_sum_exp .(Note that 1 = exp(0), as the first exp term being summed inside the log).
As listed in CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions
log_sum_exp is compatible with invoking CVXQUAD’s Padé Approximant instead of CVX’s Successive Approximation method. You can deal with the exp terms outside the log using either of the reformulations described in the just provided link for exp(cvx_expression) .
Hi,Mark, thank you very much for your reply!
I modified the above code as follows, however, it exists programming error.
The modified code is:
cvx_begin
variable x(temp)
variable z(temp)
dual variables y
minimize lambda(1)*(A(1)+B(1)z(1)-v(1)(alpha(1)/log(2)*log(gain(1)*exp(x(1))/(1+gain(2)exp(x(2))))+beta(1)))+…
lambda(2)(A(2)+B(2)z(2)-v(2)(alpha(2)/log(2)*log(gain(2)*exp(x(2)))+beta(2)))
{exp(x),1,z} == exponential(1)
subject to
y : x<=log(MaxPowerOfUE);
cvx_end
The status is :
Using Pade approximation for exponential
cone with parameters m=3, k=3
=====================================
Wrong usage: cvxprob/newcnstr (line 192)
Disciplined convex programming error:
** Invalid constraint: {log-affine} == {real affine}**
Error: cvxprob/newcnstr (line 72)
** newcnstr( prob, x{k}, y{k}, op );**
Error == (line 3)
b = newcnstr( evalin( ‘caller’, ‘cvx_problem’, ‘[]’ ), x, y, ‘==’ );
Error test_cvx2 (line 17)
** {exp(x),1,z} == exponential(1)**
I solved the above problem via modifying as follows:
cvx_begin
variable x(temp)
variable z(temp)
dual variables y
minimize lambda(1)*(A(1)+B(1)z(1)-v(1)(alpha(1)/log(2)*log(gain(1)*exp(x(1))/(1+gain(2)exp(x(2))))+beta(1)))+…
lambda(2)(A(2)+B(2)z(2)-v(2)(alpha(2)/log(2)*log(gain(2)*exp(x(2)))+beta(2)))
% {exp(x(1)),1,z(1)} == exponential(1)
% {exp(x(2)),1,z(2)} == exponential(1)
exp(x) + rel_entr(1,z) <= 0
% exp(x(2)) + rel_entr(1,z(2)) <= 0
subject to
y : x<=log(MaxPowerOfUE);
cvx_end
Hi, Mark~ I’m sorry to bother you again.
I’m confused why the follwing two replacements got different optimization results:
The first case:
I replace the exp(expression) as follows:
exp(x(1)) + rel_entr(1,z(1)) <= 0
** exp(x(2)) + rel_entr(1,z(2)) <= 0**
The result is :
Successive approximation method to be employed.
For improved efficiency, SDPT3 is solving the dual problem.
SDPT3 will be called several times to refine the solution.
Original size: 85 variables, 33 equality constraints
2 exponentials add 16 variables, 10 equality constraints
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
2/ 2 | 8.000e+00 9.068e+00 0.000e+00 | Solved
2/ 2 | 6.587e+00 2.329e+00 0.000e+00 | Solved
2/ 2 | 1.950e-01 2.376e-03 0.000e+00 | Solved
1/ 1 | 2.793e-02 2.410e-05 0.000e+00 | Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Solved
Status: Solved
Optimal value (cvx_optval): +296.698
The second case:
I replace the exp(expression) as follows:
exp(x(:)) + rel_entr(1,z(:)) <= 0
The result is:
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
2/ 2 | 8.000e+00 6.864e+00 0.000e+00 | Solved
1/ 1 | 6.229e-01 2.398e-02 0.000e+00 | Solved
1/ 1 | 1.138e-02 8.055e-06 0.000e+00 | Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Solved
Status: Solved
Optimal value (cvx_optval): +296.899
Those two results may be within solver tolerance of each other, and especially considering that it is in the context of the Successive Approximation method, which has its own termination criterion ,which I don’t know what it is. Perhaps CVX presents slightly different, but equivalent (in exact arithmetic) formulations to the solver in each of the two cases, so the solver may not produce the exact same result.
Why aren’t you using log_sum_exp ? The reformulation(s) you used for exp(cvx_expression) did invoke CVX’s Pade Approximation, as evidenced by
Using Pade approximation for exponential
cone with parameters m=3, k=3
However, because you didn’t eliminate log by using log_sum_exp,. the Successive Approximation method was still used, even though part of what the Successive Approximation method iwould have had to deal with was replaced by the Pade Approximant, thereby perhaps giving the Successive Approximation method a somewhat easier problem to deal with. BTW, those large gains might be contributing to the solution difficulty, even though they are inside a log.