How to express “minimize sup |H(ω)-D(ω)|,ω∈[0,π]” in CVX?

1

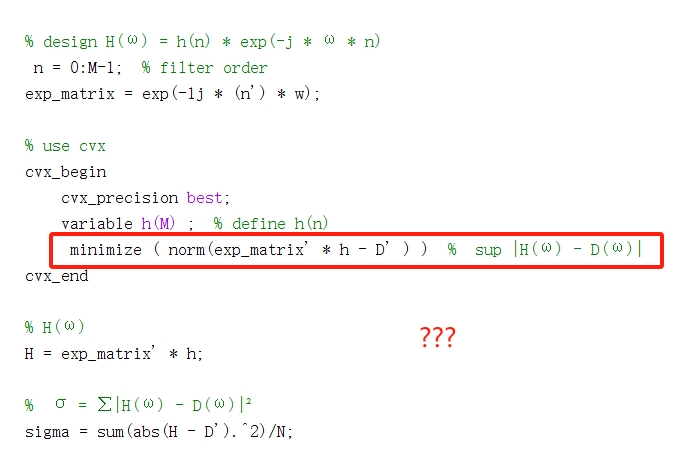
minimize sup |H(ω)-D(ω)|,ω∈[0,π]

D(ω) is known
Where sup|·| represents the lower bound; D(ω) is the ideal frequency response function; H(ω) is the desired filter frequency response function, expressed as H(ω)=h(n)exp-jωn
2) Determine the appropriate number of frequency sampling points. Uniform sampling is performed within the range of ω=[0,π]. The more sampling points, the closer to the target D(ω). Here, N=15M and M=41 are taken as the order of the filter h(n);
3) Use the cvx toolbox in MATLAB to solve the filter coefficient h(n);
4) Select the filter order, obtain H(ω) and calculate the mean square error. Define the mean square error value σ as:
σ=∑|H(ω)-D(ω)|²,
Specify σ＜10 to the power of -19

This is the simulation step for designing the filter h(n) in the paper. I want to reproduce it, but I don’t know how to express it“minimize sup |H(ω)-D(ω)|,ω∈[0,π]”

Below is my code, but the result does not match the paper

微信截图_20240926155849

2

Think of sup as being max.

So if H and D are vectors over a range of \omega values, you would have something like
minimize(max(abs(H-D)))

Change abs to what is is supposed to be, if it does not mean abs.

The above presumes that H and D` are affine with respect to the CVX )optimization) variables.

4

the paper said sup|·| as being min.
I try minimize(min(abs(H-D))) ,but it says “Disciplined convex programming error:
Invalid computation: min( {convex} )” ，how can I solve it ?

5

sup as being min makes no sense. Perhaps that is a “typo” in the paper.

minimize(min(abs(H-D))) would be a non-convex objective, and not allowed in CVX.

6

Thank you for your patience!