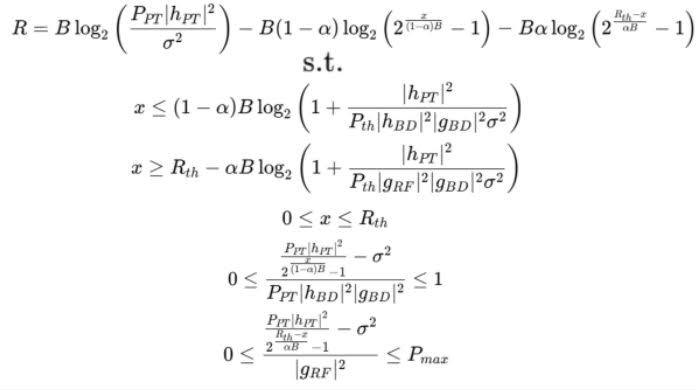x is the variale, and B is a constant.
I can not deal with the -1 term, otherwise it seems that log_sum_exp works.
This is basically (in terms of difficulty of entering in CVX) the same as log(exp(x)-1). It is concave and log-convex. I will defer to others as to whether it can be reformulated in a DCP-compliant manner.
Depending on how it is going to be used, perhaps you don’t need to enter log(exp(x)-1) But you haven’t told us how you intend to use it. You do, however, need the overall optimization problem to be convex, or transformable thereto.
Here is the objective function, where the only variable is x. And the -1 term in log function may not be ingored due to the range of x is [0, R_th].
t<=log(exp(x)-1) is equivalent to exp(t-x)+exp(-x)<=1 which you can enter directly.
1 Like