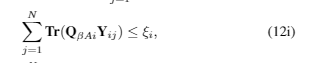Here is one of the constraint of my cvx program {\sum\limits_{j=1}^{N} \textbf{Tr}(\textbf{Q}_{\beta A i} \textbf{Y}_{ij})} {\leq \xi_i }, where \textbf{Q}_{\beta A i} is 10X10 matrix and variable \textbf{Y}_{ij} is 10X10XN matrix, how to write this constraint in CVX. Can anyone help me. Thank you.
How is the product of a 10 by 10 matrix (\textbf{Q}_{\beta A i}) with a 10 by 10 by N matrix (\textbf{Y}_{ij}) defined?
Perhaps you want Y(:,:,k), which is a 10 by 10 matrix ? Your notation and indexing seems a little confusing or wrong, but the k index for Y would be the index of summation (which you show as j).
On second thought, it appears the index of summation should be j. So then it makes no sense to have 1 3rd dimension of Y, unless perhaps the constraint needs to hold for each possible value of the index of the 3rd dimension.
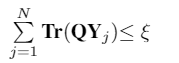
Yes, i want Y(:,:,j), I am putting it again in simple notation, Here Q is 10X10 matrix and is a constant. Y is the variable with dimension 10X10XN. I have constraint as Trace(QY(:,:,1))+Trace(QY(:,:,2)) +…+Trace(Q*Y(:,:,N))<=\xi . How can write it in CVX. Thank You.
Maybe there;s a better way, but here is a brute force way.
Summand = 0;
for j = 1:N
Summand = Summand + Q*Y(:,:,j)
end
trace(Summand) <= zeta
I’ll let you worry about the indexing with respect to i.
Summand = 0;
for j = 1:N
Summand = Summand + trace(Q*Y(:,:,j))
end
Summand <= zeta
OP asked the trace on trace(Q*Y(:,:,j)) not trace on summation.
Trace is a linear operator. So the result is the same either way.
Perhaps your way saves some CVX processing time, though? I don’t know.
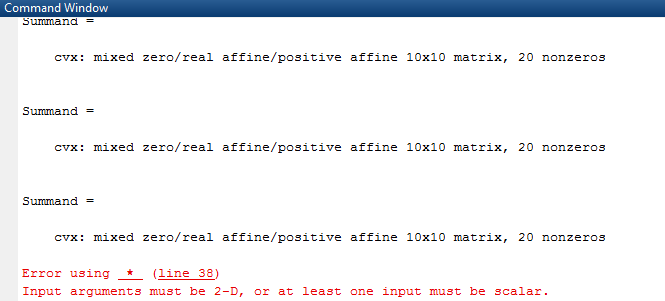
I am receiving this message after CVX run.
What value of j does the error occur at? What is shown for whos Y ? What are the contents of Y(:,:,j)f or that value of j?
if looking at that doesn’t allow you to resolve your difficulty, please show the complete reproducible progran with all input and all output.