How to express (1+det(g*w)^2+(t-1)^2/4)^(1/2)<=(t+1)/2?

1

I am trying to solve the problem below using cvx, and I am having trouble expressing the first subject expression
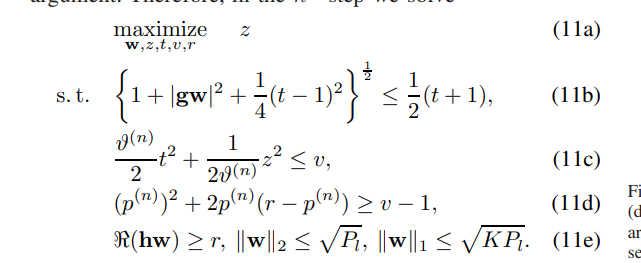
QQ图片20231217100034

2

I am a beginner in cvx, and I was using this way to express, then it report an error, could any one tell me what is wrong with it?

3

my expression :
x = [1;norm(g*w,1);(t-1)*inv_pos(2)];
norm(x,2) <= (t+1)*inv_pos(2);
error:

QQ图片20231217100523
QQ图片20231217100523897×195 5.47 KB

4

I don’t know what everything is. It looks rather dubious to me that |g*w| means det(g*w| in this case, because I strongly suspect that g*w is not a matrix. But it’s “your” problem (in the sense that you copied it from a paper or book), so you should know.

Is
norm([1;g*w;(t-1)/2]) <= (t+1)/2
correct?

BTW, your use of inv_pos(2) is not wrong, but seems to unnecessarily complicate things, so I didn’t use it. I only use inv_pos when its argument is a CVX varaible or expression, not a constant.

5

The error message is because CVX requires the argument of norm to be affine.

help cvx/norm

Disciplined convex programming information:
    norm is convex, except when P<1, so an error will result if
    these non-convex "norms" are used within CVX expressions. norm 
    is nonmonotonic, so its input must be affine.
6

you’re right, in this case g is a row vector and w is a column vector. I mistakenly thought gw is a matrix.
and norm([1;gw;(t-1)/2]) <= (t+1)/2 really worked!!! thank you very much!
(as to using inv_pos(2), this is because I once received an error on a sentence with “/” , then I changed to inv_pos, and now I know the problem is not because of “/”.Thank you again.)