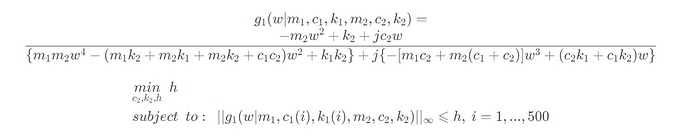Dear all,
I am sorry to bother you. Recently, I have been learning convex optimization and The DCP Rulerset. I clearly understand that I must prove the function is convex before using CVX. That’s difficult.
As we all know, p-norm is convex when p\geq 1 and that is easy to prove according to the properties of the norm.
But I have an optimization problem shown as follows:
where w is a constant vector, m_1,c_1(i),k_1(i),m_2 are constants, c_2,k_2 are scalars.
I just cannot understand a function’s infinity norm means in mathematics. I tried to find some helpful information but failed. So I want to know how to learn the a function’s infinity norm and prove it is convex or not.
Thank you very much in advance.
The Markdown code cannot display all the equations, so I paste the picture.