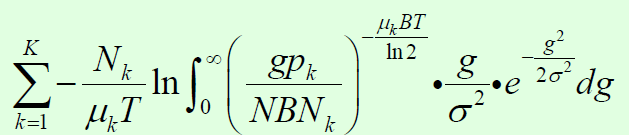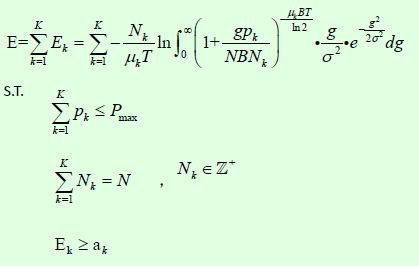How to discribe integral ,including parameter,in a function

Nonconvex
1 
    Hi,everyone.I'm looking for a function to discribe integral in CVX.Maybe my problem is too complex ,I haven't found method to solve it.
   function [ x1 x2 x3 x4 x5 x6 x7 x8 ] = MYcvx1()

A=0.1;
T=10^-3;
N=10^-4;
B=15000;
d=0.1;
%In High-SNR Situation
cvx_begin
variable x1
variable x2
variable x3
variable x4
variable x5
variable x6
variable x7
variable x8
E1=@(g,x1,x5)1./(log(2).*N).*rel_entr(g.*x5,N.*B.*x1)+x1.*g.^2./(A.*T.*2.*d.^2).*log(g./d.^2);
Q1=integral(@(g)E1(g,x1,x5),0,inf);

     E2=@(g,x2,x6)1./(log(2).*N).*rel_entr(g.*x6,N.*B.*x2)+x2.*g.^2./(A.*T.*2.*d.^2).*log(g./d.^2);
      Q2=integral(@(g)E2(g,x2,x6),0,inf);
     
    E3=@(g,x3,x7)1./(log(2).*N).*rel_entr(g.*x7,N.*B.*x3)+x3.*g.^2./(A.*T.*2.*d.^2).*log(g./d.^2);
      Q3=integral(@(g)E3(g,x3,x7),0,inf);
      E4=@(g,x4,x8)1./(log(2).*N).*rel_entr(g.*x8,N.*B.*x4)+x4.*g.^2./(A.*T.*2.*d.^2).*log(g./d.^2);
      Q4=integral(@(g)E4(g,x4,x8),0,inf);
     maximize(Q1+Q2+Q3+Q4)
     subject to
     Q1>=50000;
     Q2>=50000;
     Q3>=50000;
     Q4>=50000;
      x1+x2+x3+x4==40;
      x5+x6+x7+x8==20;
       x1>=0;
       x2>=0;
       x3>=0;
       x4>=0;
       x5>=0;
       x6>=0;
       x7>=0;
       x8>=0;

cvx_end
end

Error using integralCalc/finalInputChecks (line 511)
Input function must return ‘double’ or ‘single’ values. Found ‘cvx’.

Error in integralCalc/iterateScalarValued (line 315)
finalInputChecks(x,fx);

Error in integralCalc/vadapt (line 132)
[q,errbnd] = iterateScalarValued(u,tinterval,pathlen);

Error in integralCalc (line 83)
[q,errbnd] = vadapt(@AToInfInvTransform,interval);

Error in integral (line 88)
Q = integralCalc(fun,a,b,opstruct);

Error in MYcvx1 (line 19)
Q1=integral(@(g)E1(g,x1,x5),0,inf);

Hope to your rely.

Sincerely
JackEI

2

The MATLAB integral function is not supported in CVX. Do you even know whether your optimization problem is convex? Are you able to determine closed form solutions or approximations for the integrals?

3

I’m glad to receive your rely.The convexity of this problem has been proved by others.so,i want to know whether there is a discription for integral in CVX,or there are other methods to solve my problem.Thank you.

Pk,Nk are invariable,the other are constant.

4

Have you examined the convexity proof? Does that give you any clues as to how to formulate your problem in a CVX-compliant manner?

If I had a dollar for each instance in which someone on this forum claimed a function was convex when it really wasn’t … I’d have several dollars … so I reserve a healthy skepticism.

5

I will not rule out that this is convex, if only because I do not have the time to prove or disprove it.

I am putting this in the Nonconvex bin anyway. Because if you had read the FAQ as instructed, or even better the documentation, you would not even be attempting to solve this model in CVX.

6

Maybe I need to examine the convexity again,or I need find other method to solve it.
Thank you Mark.

7

It’s not just convexity that’s the issue here. It is the disciplined aspect of CVX that prevents you from using it. That is what the documentation and FAQ explain.

8

Thank you mcg.Do you give me some advice to solve it ? If i can add some constrains,whether it can find optimal solution.

9

I’m sorry to ask you for my problem again.I have modified my objective function below.can you give me some advice to describe it ? I have proof it about its convexity.Thank you.