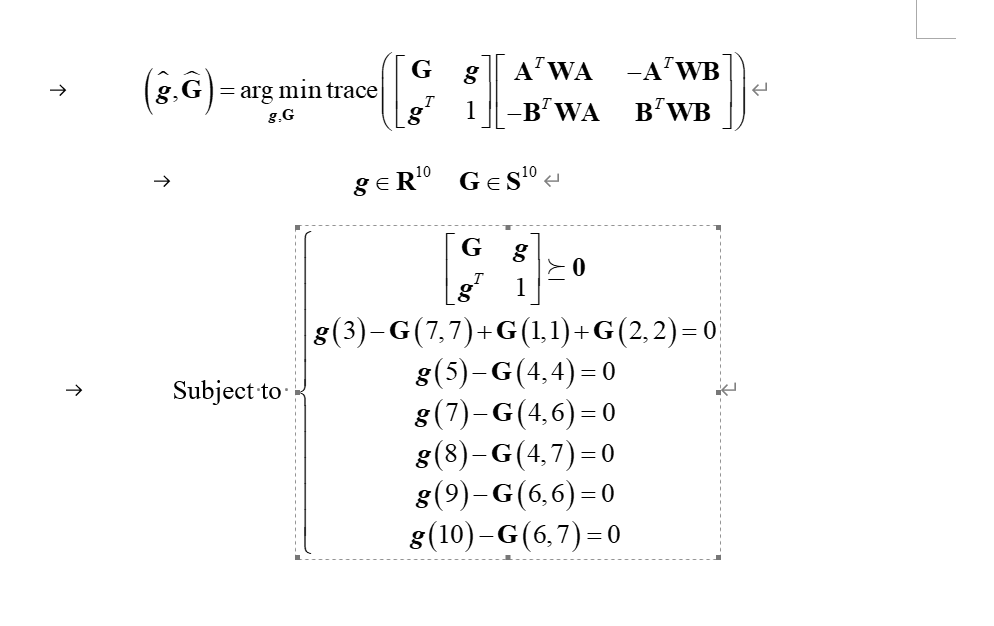
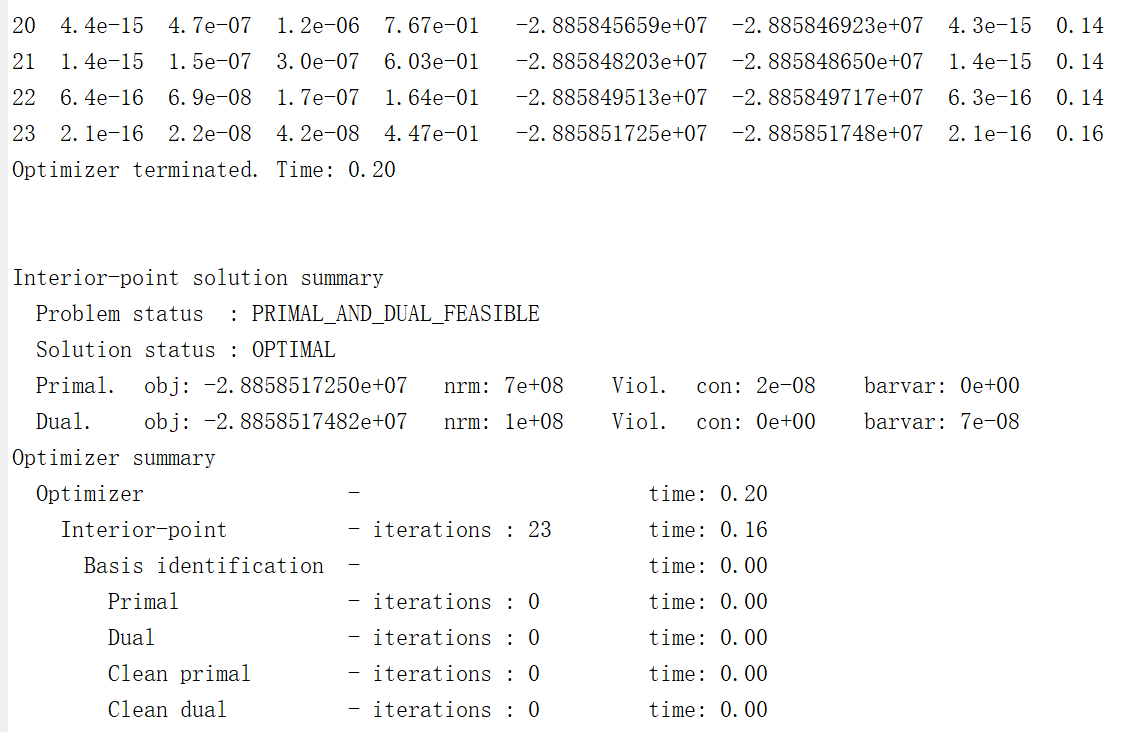
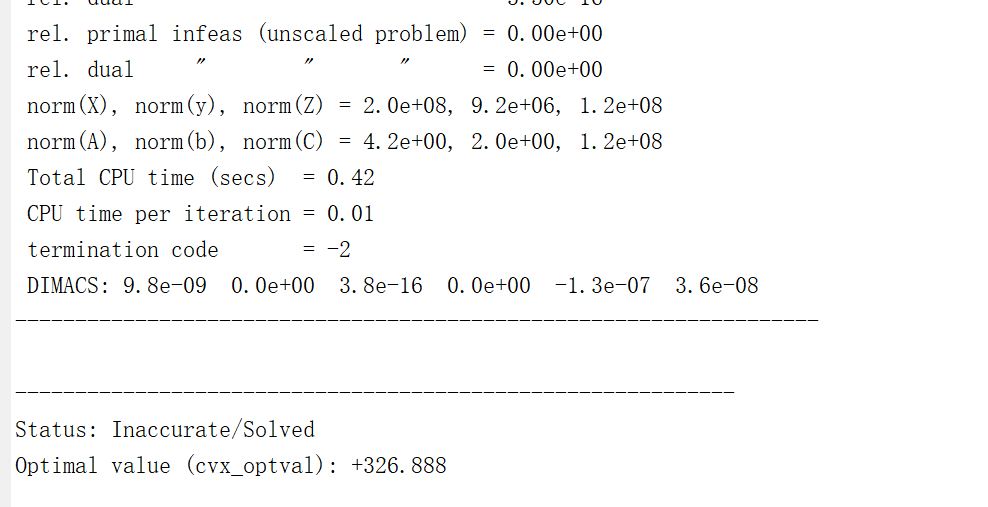hi, everyone, this is my problem
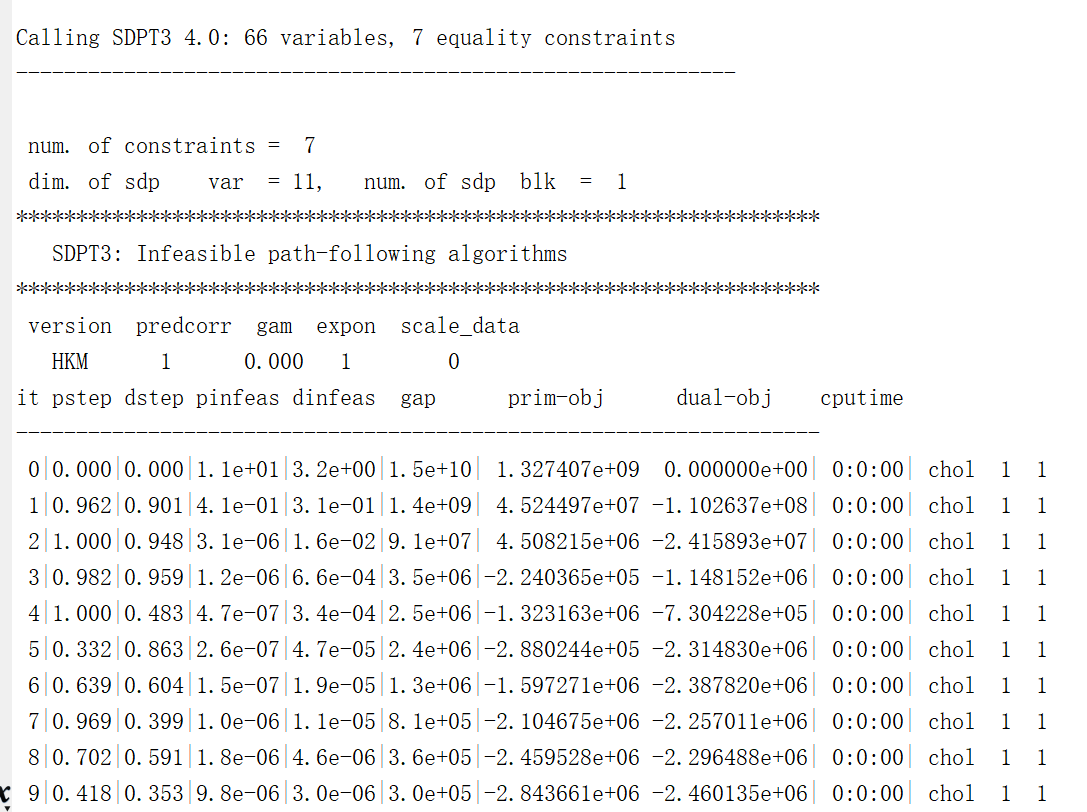
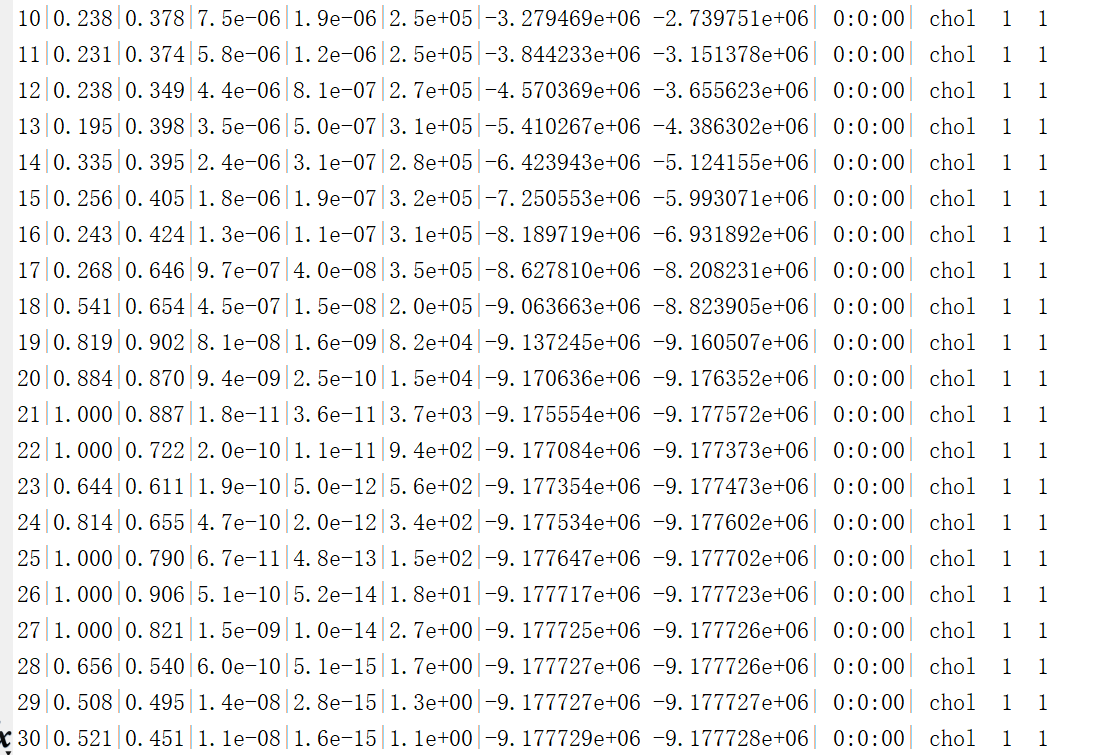
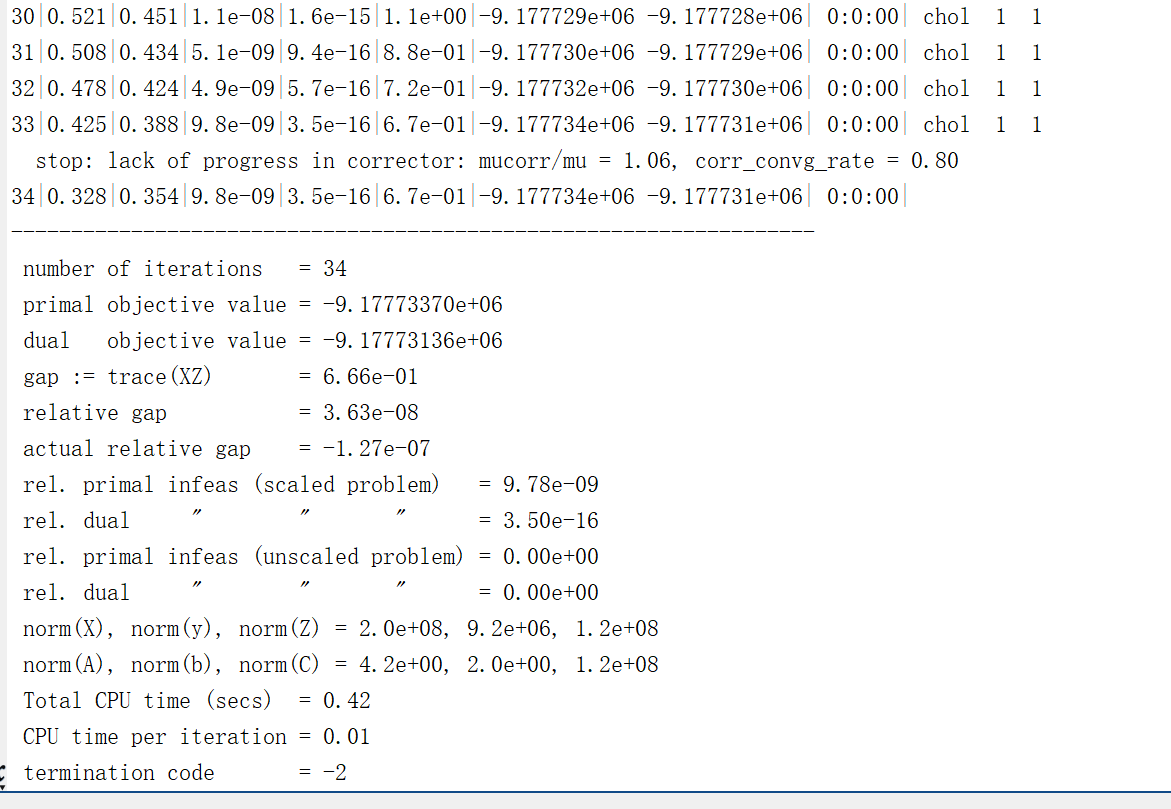
I try to solve it with CVX toolbox, the status is Inaccurate/Solved, the following is my code.
clc
clear all
close all
format long
%% Trajectory
T=10; % 信号发射周期
v=10*0.54444; % 在定位测量点时水面船的运动速度
Radius=2.51000; %%%% 圆形轨迹的半径
ArcAngle=vT/Radius;
Angle=0:ArcAngle:(2pi+ArcAngle);
PosLoc=[Radiuscos(Angle(1:end-1));Radius*sin(Angle(1:end-1))];
PosLoc=PosLoc’;
xShip=PosLoc(:,1)+10randn(size(PosLoc(:,1)));
yShip=PosLoc(:,2)+10randn(size(PosLoc(:,1)));
zShip=0; % 发射换能器的入水深度
%% Target
Range=[800:100:1000];
xTar=Range/sqrt(2);
yTar=Range/sqrt(2);
NN=length(Range); % 阵元数目
zTar=50;
%% measurement error
detat=10.001; % 时延测量误差
tb=50.001;
c=1500+5*randn(size(xShip));
cb=5; % 声速测量的固定偏差
detac=1; % 声速测量 随机误差的标准差
detaa=1; % 节点位置的随机误差
%% solving
RmseCWLLS1=zeros(1,length(xTar));
xErr=zeros(1,length(xTar));
yErr=zeros(1,length(xTar));
for nn=1:NN
nn
for mc=1
mc
xShipMea=xShip+detaa*randn(size(xShip));
yShipMea=yShip+detaa*randn(size(yShip));
tMea=sqrt((xShip-xTar(nn)).^2+(yShip-yTar(nn)).^2+(zShip-zTar).^2)./c+detat*randn(size(xShip))+tb;
cMea=ones(size(xShip)).*(c+cb+detac*randn(size(xShip)));
%% SDP
A=[2*xShipMea,2*yShipMea,ones(length(xShip),1),-2*tMea.^2.*cMea,tMea.^2,-2*tMea.*cMea.^2,4*tMea.*cMea,-2*tMea,cMea.^2,-2*cMea];
B=xShipMea.^2+yShipMea.^2+(zShip-zTar)^2-tMea.^2.*cMea.^2;
rk=sqrt((xTar(nn)-xShip).^2+(yTar(nn)-yShip).^2+(zTar-zShip)^2);
wt=detat^2*diag(4*rk.^2.*c.^2);
wxy=detaa^2*diag(4*rk.^2);
wc=detac^2*diag(4*rk.^2.*(rk./c).^2);
W=eye(length(tMea))/(wt+wxy+wc);
Coe=[A'*W*A -A'*W*B;-B'*W*A B'*W*B];
cvx_begin sdp
cvx_precision high
variable G(10,10) symmetric;
variable g(10);
minimize(trace([G g;g' 1]*Coe));
subject to
[G g;g' 1] >= 0;
g(3)-G(7,7)+G(1,1)+G(2,2) == 0;
g(5)-G(4,4) == 0;
g(7)-G(4,6) == 0;
g(8)-G(4,7) == 0;
g(9)-G(6,6) == 0;
g(10)-G(6,7) == 0;
cvx_end
X(1,1)=xTar(nn);
X(2,1)=yTar(nn);
X(3,1)=tb^2*cb^2-xTar(nn)^2-yTar(nn)^2;
X(4,1)=cb;
X(5,1)=cb^2;
X(6,1)=tb;
X(7,1)=tb*cb;
X(8,1)=tb*cb^2;
X(9,1)=tb^2;
X(10,1)=tb^2*cb;
xSDP_g(mc,nn)=g(1);
ySDP_g(mc,nn)=g(2);
xSDP_G(mc,nn)=sqrt(G(1,1)); %%%% 这块需要讨论使用G中数据还是g中的数据
ySDP_G(mc,nn)=sqrt(G(2,2));
end
end
RmseSDP_g=sqrt(sum((xSDP_g-ones(mc,1)*xTar).^2+(ySDP_g-ones(mc,1)*yTar).^2,1)./mc);
RmseSDP_G=sqrt(sum((xSDP_G-ones(mc,1)*xTar).^2+(ySDP_G-ones(mc,1)*yTar).^2,1)./mc);
BiasSDP_g=sqrt((mean(xSDP_g-ones(mc,1)*xTar,1)).^2+(mean(ySDP_g-ones(mc,1)*yTar,1)).^2);
BiasSDP_G=sqrt((mean(xSDP_G-ones(mc,1)*xTar,1)).^2+(mean(ySDP_G-ones(mc,1)*yTar,1)).^2);
%% 绘图和保存数据
figure;
hold on
scatter(xShip,yShip,‘blue.’);
scatter(xTar,yTar,‘red.’);
legend(‘校阵节点’,‘水听器位置’)
xlabel(‘x(m)’);
ylabel(‘y(m)’);
xlim([-3000 3000])
ylim([-3000 3000])
axis equal
grid on
box on
figure;
hold on
plot(Range,RmseSDP_g,‘black-<’,‘LineWidth’,1.5)
plot(Range,RmseSDP_G,‘red->’,‘LineWidth’,1.5)
box on
grid on
set(gca,‘GridLineStyle’,‘–’)
xlabel(‘Distance(m)’)
ylabel(‘RMSE(m)’)
figure;
hold on
plot(Range,BiasSDP_g,‘black-<’,‘LineWidth’,1.5)
plot(Range,BiasSDP_G,‘red->’,‘LineWidth’,1.5)
box on
grid on
set(gca,‘GridLineStyle’,‘–’)
xlabel(‘Distance(m)’)
ylabel(‘Bias(m)’);
% for Num=1:NN
% figure;
% hold on
% scatter(xSDP_g(:,Num),ySDP_g(:,Num),‘black.’);
% scatter(xSDP_G(:,Num),ySDP_G(:,Num),‘black.’);
% scatter(xTar(Num),yTar(Num),‘green*’);
% end