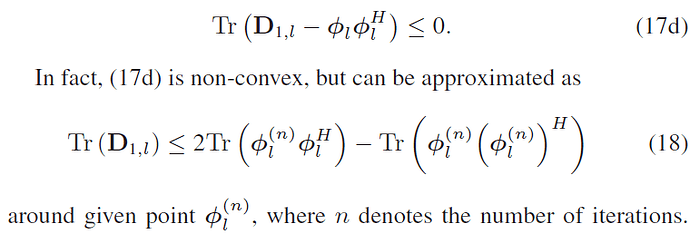Hi, I am having a bit of trouble reproducing a paper.
The formula below is the constraint given in the paper after the relaxation, which according to the paper should be convex.
\operatorname{Tr}\left(\mathbf{D}_{1, l}\right) \leq 2 \operatorname{Tr}\left(\phi_{l}^{(n)} \phi_{l}^{H}\right)-\operatorname{Tr}\left(\phi_{l}^{(n)}\left(\phi_{l}^{(n)}\right)^{H}\right)
where \phi_{l} is the variable to be optimized, \mathbf{D}_{1, l} is a known complex matrix, n represents the number of iterations and \phi_{l}^{(n)} is a given point at n-th iteration.
But when I run the simulation in matlab with CVX, I have this problem
Disciplined convex programming error:
Invalid constraint: {complex affine} >= {complex number}
I would like to ask what to do in such a case? Is it because there is something wrong with my code? I hope I can get your answer.
In case my description is incorrect, I give below the description of this constraint from this paper.
1 Like
CVX does not allow complex inequalties.
You haven’t told us everything, nor shown us your code or input data.
Are each side of the inequality supposed to be real, at least if evaluated in exact arithmetic? If not, is the inequality to be interpreted as applying separately to both the real and imaginary parts?
If the former, use real(LHS) <= real(RHS)
If the latter use real(LHS) <= real(RHS), imag(LHS) <= imag(RJS)
http://cvxr.com/cvx/doc/dcp.html#constraints
One or both sides of an equality constraint may be complex; inequality constraints, on the other hand, must be real. A complex equality constraint is equivalent to two real equality constraints, one for the real part and one for the imaginary part. An equality constraint with a real side and a complex side has the effect of constraining the imaginary part of the complex side to be zero.