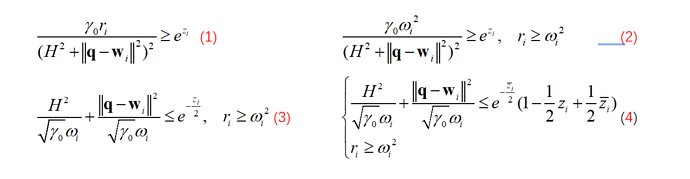How to deal with {convex} ./ {real affine} or {convex} .* {convex}}

1

If someone helped me, I would be very grateful.
In the picture, z, r and q are variables. I first use \omega to replace r like (2). Then we can get (3). The LHS of (3) is convex with respect to \omega and q(I have certificated it). The RHS of (3) is also convex with respect to z. So I employ the first-order approximation technique to the RHS of (3) and we can get (4).
The two constraints are convex. I also use inv_pos() function. However, when I use cvx to solve it, cvx reminds Cannot perform the operation: {convex} .* {convex}.
Please help me.

1342×349 10.9 KB

2

If I understand what your problem is, and I’m not sure I do, I think you can use quad_over_lin

help quad_over_lin

quad_over_lin Sum of squares over linear.
Z=quad_over_lin(X,Y), where X is a vector and Y is a scalar, is equal to
SUM(ABS(X).^2)./Y if Y is positive, and +Inf otherwise. Y must be real.

If X is a matrix, quad_over_lin(X,Y) is a row vector containing the values
of quad_over_lin applied to each column. If X is an N-D array, the operation
is applied to the first non-singleton dimension of X.

quad_over_lin(X,Y,DIM) takes the sum along the dimension DIM of X.
A special value of DIM == 0 is accepted here, which is automatically
replaced with DIM == NDIMS(X) + 1. This has the effect of eliminating
the sum; thus quad_over_lin( X, Y, NDIMS(X) + 1 ) = ABS( X ).^2 ./ Y.

In all cases, Y must be compatible in the same sense as ./ with the squared
sum; that is, Y must be a scalar or the same size as SUM(ABS(X).^2,DIM).

Disciplined convex programming information:
    quad_over_lin is convex, nonmontonic in X, and nonincreasing in Y.
    Thus when used with CVX expressions, X must be convex (or affine)
    and Y must be concave (or affine).
3

Thank you very much. The problem is solved.