In the picture, Psi is the variable.
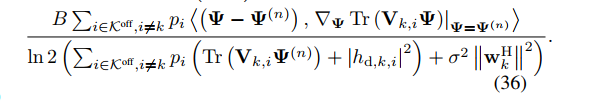
my code is as follows
D2_fraction_all_1(a_off(k))/((log(2))*(D2_2(a_off(k))))
where D2_fraction_all_1(a_off(k)) is the numerator ,((log(2))*(D2_2(a_off(k)))) is the denominator.
In the picture, Psi is the variable.
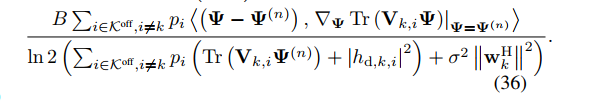
my code is as follows
D2_fraction_all_1(a_off(k))/((log(2))*(D2_2(a_off(k))))
where D2_fraction_all_1(a_off(k)) is the numerator ,((log(2))*(D2_2(a_off(k)))) is the denominator.
We don’t know how this is used in your optimization problem. But your first task is to prove that your optimization problem is convex.
Thanks, I solved this problem, but I have the problem now.
My problem is
d1_all = 0;
d2_all =0;
Psi_hat_ini = Psi_hat;
D2_fraction_all =0;
cvx_begin
variable Psi_hat(M+1, M+1) hermitian
%%%%% Paramenter generation %%%%%cvx_solver mosek
% -------------D2,k----------------
for k=1 : length(a_off)
h_IRS_1(a_off(k), :)= W_ini(:, a_off(k))‘G(:,:,a_off(k));
h_d_1(a_off(k)) = W_ini(:, a_off(k))‘H_UB (:, a_off(k));
V(:, :, a_off(k)) = [h_IRS_1(a_off(k),:)'h_IRS_1(a_off(k), :), h_IRS_1( a_off(k),:)'h_d_1(a_off(k)); h_d_1(a_off(k))’ h_IRS_1(a_off(k),:) zeros(1)];
V2_2(a_off(k)) = (real(trace((V(:, :, a_off(k))) Psi_hat_ini)) + real((h_d_1(a_off(k))))^2);
d2(a_off(k))= trans_power_ini(a_off(k))real(V2_2(a_off(k)));
d2_all = d2_all +d2(a_off(k));
D2_fraction(:, a_off(k)) = trans_power_ini(a_off(k))dot((Psi_hat - Psi_hat_ini) ,V(:, :, a_off(k)));
D2_fraction_all = D2_fraction_all + D2_fraction(a_off(k));
end
for k=1 : length(a_off)
aa((a_off(k))) = (noise_maxpower^2)(norm(W_ini(:, (a_off(k)))', ‘fro’))^2;
D2_1(a_off(k)) = Blog(d2_all - d2(a_off(k)) + aa((a_off(k))))/(log(2)) ;
D2_2(a_off(k)) = d2_all - d2(a_off(k)) +(noise_maxpower^2) (norm(W_ini(:, (a_off(k)))’, 2))^2;
D2_fraction_all_1(a_off(k)) = B(D2_fraction_all - D2_fraction(a_off(k)));
end
for k=1 : length(a_off)
D2_estimation(a_off(k)) = D2_1(a_off(k)) +D2_fraction_all_1(a_off(k))(((log(2))((D2_2(a_off(k)))))^-1);
end
% -------------D1,k----------------
for k=1 : length(a_off)
V1(a_off(k)) =(real(trace((V(:, :, a_off(k)))* Psi_hat)) + real((h_d_1(a_off(k))))^2);
d1(a_off(k))= trans_power_ini(a_off(k))real(V1(a_off(k)));
d1_all = d1_all +d1(a_off(k));
end
for k=1 : length(a_off)
aa((a_off(k))) = (noise_maxpower^2)(norm(W_ini(:, (a_off(k)))’, ‘fro’))^2;
D1_1((a_off(k))) = d1_all +aa(a_off(k));
D1((a_off(k))) = Blog(D1_1(a_off(k)))/(log(2)) ;
end
% -------------Rate----------------
for k=1 : length(a_off)
rate_estimation(a_off(k)) = (real(D1((a_off(k)))) - real(D2_estimation(a_off(k))));
end
% -------------Constraint----------------
for k=1 : length(a_off(k))
constraint_1(a_off(k)) = mu(trans_power_ini(a_off(k))*user_data_amount(a_off(k))*inv_pos(rate_estimation(a_off(k))) ) - xi_Phi;
constraint_2(a_off(k)) = user_data_amount(a_off(k))*inv_pos(rate_estimation(a_off(k)) ) + user_circle(a_off(k))/ F_c_ini(a_off(k)) - T_MAX;
end
subject to
real(constraint_1) <= 0;
real(constraint_2) <= 0;
Psi_hat == hermitian_semidefinite(M+1);
diag(Psi_hat) ==1;
cvx_end
This is what I ran
I want to know if there is a problem with this run result, I think there should be a problem, because both constraints result in 0, but when I examine the run result in detail, I find that the second term of D1 is 0 (actually should be a number).
I don’t what your model results “should be”. It is a feasibility problem, so the solver and CVX can report whichever feasible solution they want, whether or not it is the same as the feasible soiution in some book or paper.
I don’t know what you mean by " the second term of D1 is 0 (actually should be a number)." Zero is a number. Do you mean it should be a non-zero number?
Please show us the output, and describe very clearly, what you think might not be “right”, and why that is the case.
Note that CVX may not show the “final” value of expressions, such as D1. The only way to be guaranteed to get the final (optimal) values of expressions is to recompute them after CVX ends, starting with the optimal values of the CVX variables (Psi_hat).
It seems you may have gotten away with not declaring D1 and some other things as expression. I recommend you do so, per http://cvxr.com/cvx/doc/basics.html#assignment-and-expression-holders .
Thank you for your reply.This is my output:
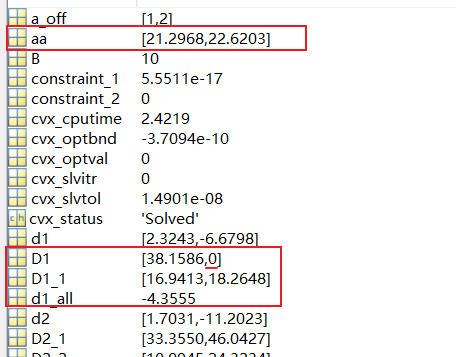
According to the calculation formula of D1, both d1_all and the second term aa have non-zero values, and D1_1 also has non-zero values, so I think the second term of D1 may be a non-zero value.And the formula for D2_1 is similar to D1, but the second term of D2_1 is not equal to 0
I am not following what you are saying., But first, pay attention to what I already wrote:
Note that CVX may not show the “final” value of expressions, such as D1. The only way to be guaranteed to get the final (optimal) values of expressions is to recompute them after CVX ends, starting with the optimal values of the CVX variables (Psi_hat).
It seems you may have gotten away with not declaring D1 and some other things as expression. I recommend you do so, per The Basics — CVX Users' Guide .
Ok,I will try it,thanks~
I have solved the above problems and my running results are as follows
And then I have a question, should I introduce auxiliary variables to make my problem converge faster? (Makes me to avoid the initial point issue in my alternate feasibility optimization problem)
If CVX reports Status solved, you should consider the problem to be solved. cv_optval = -5.59429e-10 could be due to solver tolerance. From the solver’s standpoint, and hence from CVX’s standpoint, it is “the same” as exactly zero.
OK, thank you very much!
should I introduce auxiliary variables to make my problem converge faster?
I don’t know how you want to use auxiliary variables, so I can’t answer that.
Ok, thank you for your reply.