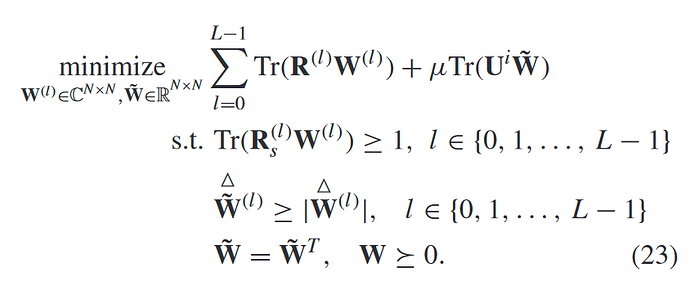How to avoid the error "value of type 'cvx' is not convertible to 'double'."

1

When I try to run the program, Matlab reports the error “Unable to perform assignment because value of type ‘cvx’ is not convertible to ‘double’.”

I tried to define U as ‘expression’ to avoid it, but actually U needs to be used in the iterative process. And when I did that, the program will report another error “An objective has already been supplied for this problem.”

I can’t understand what happened, and don’t know how should I do next.

Hope for your solutions! Thank you faithfully.

The problem needs to solve is:

1
1844×344 25 KB

And W with ‘~’ is the maximum value of the absolute value of matrix W’s elements.

The following is part of my program:

cvx_begin sdp
% cvx_solver sdpt3
    variable W(L,N) complex;
    expression U(N,N);
    expression vector(N,1);
    for l = 1:L
        wl = W(l,:);
        s_judge(l) = L - length(find(wl));
        % s_judge(l) = sum(wl ~= 0);
    end
    while (s_judge ~= P)
        mu = 1/2*(mu_min + mu_max);
        total = 0;
        total_s = 0;
        for l = 1:L
            wl = W(l,:);
            W_l = toeplitz(wl,conj(wl));
            % W_l = wl*wl';
            W_aux = max(abs(wl)) * ones(N,N);
            for p = 1:N
                for q = 1:N
                    R_l(p,q) = Rl(l,p,q);
                    Rs_l(p,q) = Rl_s(l,p,q);
                end
            end
            total = total + real(trace(R_l*W_l)) + mu * real(trace(U*W_aux));
            total_s = total_s + trace(Rs_l*W_l);
        end

        minimize total;
        subject to 
        real(trace(total_s)) >= 1;
        for l = 1:L
            wl = W(l,:);
            W_l = toeplitz(wl,conj(wl));
            lambda_p = lambda_max(W_l);
            W_l * vector == lambda_p * vector;
            prc_vector(:,l) = vector;
            % prc_vector(:,l) = V_Wl(1,:);           % prc_vector --- principal vector of W^(l)
            W_aux = max(abs(wl)) * ones(N,N);
            W_l >= 0;
            W_aux = W_aux.';
            % triu(W_aux) >= triu(W_l);
        end
        y = 1/L * sum(prc_vector,2);
        Y = toeplitz(y,y);
        for m = 1:N
            for n = 1:N
                tmp = Y(m,n) + epsilon;
                U(m,n) = inv_pos(tmp);
            end
        end

        if s_judge > P
            mu_min = mu;
        else s_judge < P;
            mu_max = mu;
        end
    end
cvx_end
2

minimize total is inside a while loop, so it might be executed more than once. Based on the error message you received, it is executed more than once. Hence the error message “An objective has already been supplied for this problem".

There should only be one occurrence of minimize (or maximize) between cvx_begin and cvx_end. If you need to build up the objective function, you should do that until you reach the final value of whatever expression you are minimizing, then have a single (execution of) minimize statement.

Your program is very confusing, and I have not put in the effort to understand it. I don’t understand the notation, such as what the triangle over the variables means. Do you mean W_tilde = norm(W(:),'inf') ? I don’t see any semidefinite constraint on W.

Your program as written makes no sense, but I don’t know what does. I have no idea what the iterative process is for. Perhaps you mean to have an iterative process outside (i.e., around) cvx_begin to cvx_end, not inside it? I.e., you want to solve a sequence of different optimization problems? if so, is that necessary? i don’t know, because I don’t understand what the overall optimization problem is.

3

Thanks for your reply and it has given me some insight. I understand why the program reports error now and maybe have another way to write the program.
Actually, the iterative process is used to search the P sparse vector w, but I think I should do that through adding relative constrain.
And triangle means the upper triangle matrix of W, it is used to constrain the values of the matrix W.
Finally, thanks for the reminder, I will the semidefinite constraint on W and it is necessary to do that.