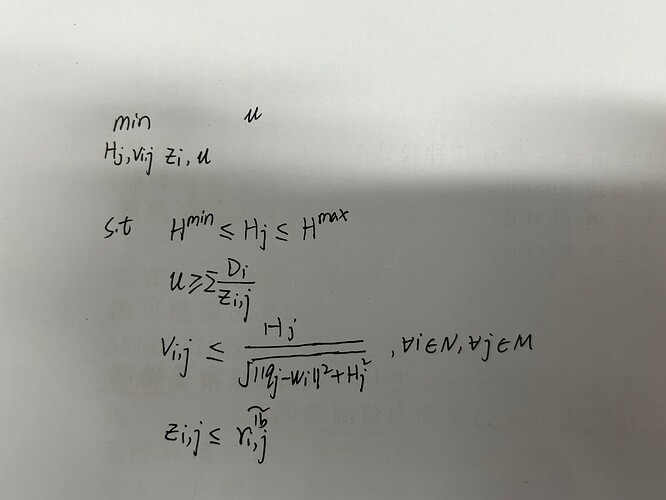In my optimization (Figure 1 below), (q-w)^2 is a constant. Which v < = H/sqrt ((q - w)^2 + H ^ 2) for variable v and H are convex (can proof) ,when I express constraints v < = H/sqrt ((q - w)^2 + H ^ 2), I try to use the H/sqrt ((q - w) ^ 2 + H ^ 2) or H/(norm ([sqrt ((q - w)); H])) or H.*inv_pos(norm([sqrt((q-w)) H]), both failed. How should I express this?Thank you very much for your help!
In order to be c convex constraint, the RHS of the inequality needs to be concave. The RHS of the inequality is convex for x <= 0 and concave for x >= 0. Therefore, it is not concave over the entirety of its natural domain. Therefore, I think it is unlikely that anyone will come up with a formulation which CVX will accept, even is x is constrained to be >= 0.
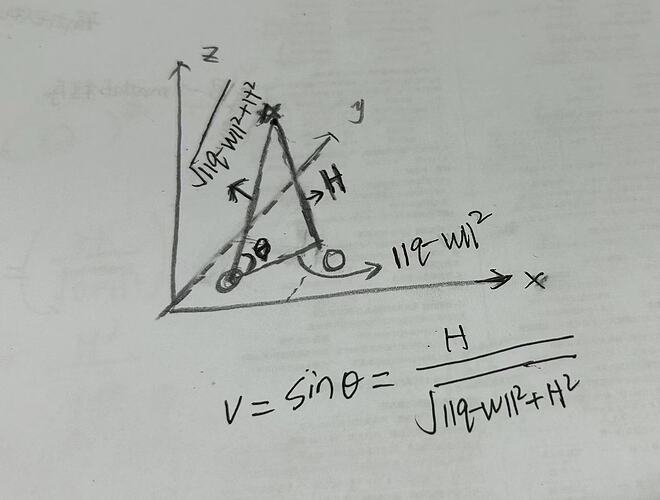
Thank you, Mark. It’s my pleasure to have your reply. Your analysis is quite correct. So because RHS is not concave over the whole natural domain, CVX doesn’t accept this expression, right? Because I’m thinking about three-dimensional coordinates, as shown below. q varies when H and w are constant, this case v<=H/sqrt((q-w)^2+H^2) is non-convex, which I can solve using a successive convex approximation, but H varies when q and w do not change. v<=H/sqrt((q-w)^2+H^2) is convex for v and H, is there any other way I can transform this so that it’s acceptable for cvx? Or can I consider using the cvx_begian gp pattern? If you have any ideas, thank you very much for giving me some advice.
You might want to consider using a non-convex optimizer, for instance under YALMIP.
If you come up with an SCA scheme, you’re on your won as far as getting to to work, it ti can work at all.
Ok, I see. Thank you very much for your help. I really appreciate what you’ve done for me.