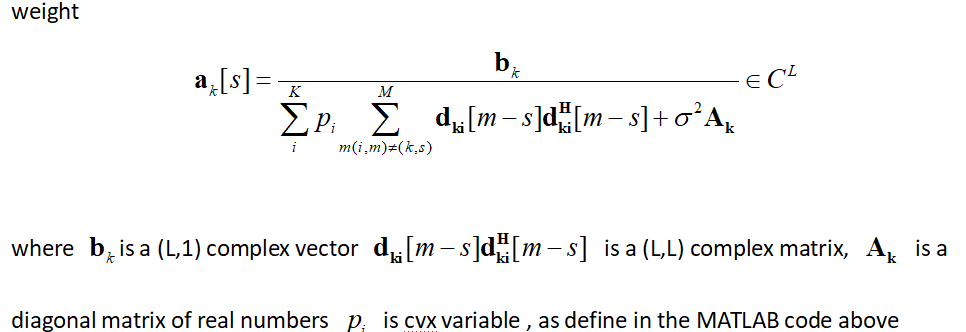How do I invert a matrix with a cvx variable if I can't use the pinv function?

Nonconvex
1

cvx_begin quiet
variable p(K,1)
expression weight(L,K,M);
expression f_n(K,M)
expression f_n_part1(K,M)
for s = 1:M
for k = 1:K
for i = 1:K
for m = 1:M
if i==k&&m==s
term2(:,:,k,i,s,m) = 0;
else
term2(:,:,k,i,s,m) = dki(:,k,i,s,m)*dki(:,k,i,s,m)';
end
end
weight(:,k,s) = pinv(squeeze(sum(p(i,1)sum(term2(:,:,k,:,s,:),6),4))+sigma2A(:,:,k))*b(:,k);
end
end
end

command-line window：
Incorrect use of svd
The first input must be a single or double precision value.

Error pinv (line 18)
[U,S,V] = svd(A,‘econ’);

Q:How do I invert a matrix with a cvx variable if I can’t use the pinv function?

2

You can’t in general, but there are limited circumstances in which it is possible. For instance, matrix_frac(x,Y) for x'*inv(Y)*x for psd Y. Also trace_inv and det_inv.

Please carefully read Why isn't CVX accepting my model? READ THIS FIRST! and CVX Users’ Guide - you will not find inv or pinv in there.

1 Like
5

屏幕截图 2024-04-20 220022
屏幕截图 2024-04-20 220022966×332 8.42 KB

Hi Mark, I’m stumped by this question.
I need to calculate a_k[s], but this inevitably contains the cvx variable p_i in the numerator, which results in no way for me to use inv(), or any other inv function. Is there any way to avoid using inv() function and calculate the value of a_k[s]?
[/quote]

6

I don’t even understand what that is,. It appears to be a vector divided by a matrix. Do you mean a_k(s) = inv(denominator)*b_k?

Did you read the links in my previous post? Whatever this is supposed to be, how is it a part of a convex optimization problem?

1 Like
7

yeah, I mean a_k(s) = inv(denominator)*b_k, I have already read your post before and carefully read the function of matrix_frac(x, Y) and trace_inv det_inv. But I can not figure out a way to calculate a_k(s) = inv(denominator)*b_k.

how is it a part of a convex optimization problem?
In my optimization constraint, I’m going to use a_k[s], so here I want to calculate it right after I define cvx variable p(K,1)

8

You have not shown that this is a convex optimization problem. If it is not, CVX is not applicable.

Please carefully reread Why isn’t CVX accepting my model? READ THIS FIRST!

If, however, a_k(s) were known, i.e., an input (which from your description it sounds like it is not), you could enter the complex affine (linear) equality constraint denominator*a_k(s) == b_k.

1 Like
9

Appreciate your help and patience, I will read this first and try another way to solve this constraint problem. Thank you!