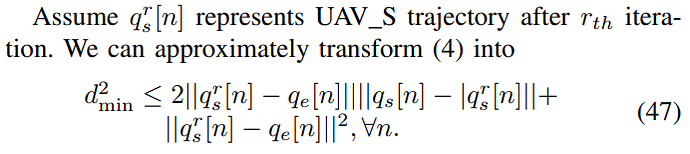The paper :
Part of My code :
for n = 1: N+1
d_min^2 <= norm(qsr(n,: ) - qe(n,: ),2)^2 + 2 * norm(qsr(n,: ) - qe(n,:),2) * norm(qs(n,: ) - qsr(n,: ),2)
end
In this,the qs is a variable,is a N+1 * 2 marix which should store n+1 coordinates.others are constants.
The error:
Disciplined convex programming error:
Invalid constraint: {real constant} <= {convex}
error <= (line 21)
b = newcnstr( evalin( ‘caller’, ‘cvx_problem’, ‘[]’ ), x, y, ‘<=’ );