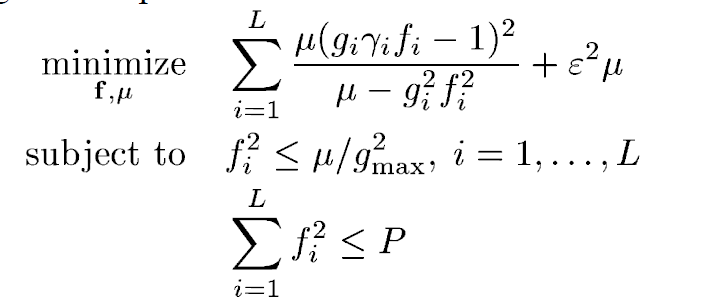How can I solve this problem in CVX?

Nonconvex
1

I want to solve a problem like this

image
image710×308 8.39 KB

Here is my cvx code

cvx_begin sdp quiet 
variable f(Ns)
variable MU_mu
expression func_obj(Ns+1)
func_obj(1) = MU_mu*varepsilon^2;
for ii = 1:Ns
    func_obj(ii+1) = func_obj(ii) + MU_mu*( g(ii)*h(ii)*f(ii) - 1 )^2 * inv_pos(MU_mu - g(ii)^2*f(ii)^2);
end
minimize func_obj(Ns+1)
subject to
    for ii = 1:Ns
        f(ii)^2 <= mu / g_max^2
    end
    f.' * f <= P_max

cvx_end

Here is error information

Disciplined convex programming error:
Cannot perform the operation: {real affine} .* {convex}

出错 * (第 36 行)
z = feval( oper, x, y );

出错 prec_proposed_BB_CSI_alg2_CVX (第 20 行)
func_obj(ii+1) = func_obj(ii) + MU_mu*( g(ii)*h(ii)f(ii) - 1 )^2 * inv_pos(MU_mu - g(ii)^2f(ii)^2);

How to solve this problem in CVX?

2

Have you proven the objective is convex? Until you have, I will assume it is not.

3

It’s really a convex problem.

4

Please sho9w us the proof. Bur before you do, please re-read the link.