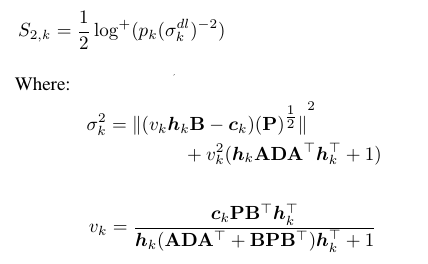How can I solve this optimization problem using cvx

Nonconvex
1

cvx
I used the following code to solve this problem

%System parameters:
N = 2;
K = 8;
M = 4;
C_l=4;
H = [0.1185 0.2811; 0.3550 0.8224; 0.3260 0.9644; 0.5333 0.6083; 0.6871 0.2298; 0.2594 0.8361; 0.1309 0.2454; 0.4715 0.2111]; %(K,N) matrix
A = [-1 1; 1 0]; %(N,N) integer matrix
C = [0 -1 1 1; 0 -1 1 1; 0 1 -1 0; 0 1 -1 0; -1 0 1 -1; -1 0 1 -1; 1 0 0 -1; 1 0 0 -1]; %(N,M) integer matrix
P = 125*eye(M); %(M,M) diagonal matrix
P_u = 125*eye(K); %(K,K) diagonal matrix
S1 = [0.5623    0.5610    0.8769    0.6921    0.8645    0.8924    0.8373    0.8927]; %(1,K) vector
% I want to find matrix B with dimensions N*M that minimizes the difference
% between S2 and S1 vectors.
cvx_begin
  variable B(N,M)
    %calculate S2 from B and the other given inputs
        for j=N:-1:1
            d(j) = (B(j,:)*P*B(j,:)')/((2^(2*C_l))-(norm(A(j,:))^2));
        end
        D = diag(d);        
        for i=K:-1:1   
            V(i)=C(i,:)*P*B'*H(i,:)'*inv(1+H(i,:)*(A'*D*A+B*P*B')*H(i,:)');
            sigma(i)=norm((V(i)*H(i,:)*B-C(i,:))*(P^(1/2)))^2+(V(i)^2)*(1+H(i,:)*A'*D*A*H(i,:)');           
            S2(i)=0.5*(log2((P_u(i,i))/(sigma(:,i))));
        end
  minimize(sum(S2-S1).^2)
  subject to
  for k=1:1:K
      S2(k) >= S1(k);
  end
cvx_end

I received the following error:

Error using  *  (line 126)
Disciplined convex programming error:
    Only scalar quadratic forms can be specified in CVX
.

Error in doOptimization3 (line 24)
            V(i)=C(i,:)*P*B'*H(i,:)'*inv(1+H(i,:)*(A'*D*A+B*P*B')*H(i,:)');

Can anyone help me to modify my code to solve this problem as I am a beginner in using cvx?

2

I have no idea what mathematical problem you are trying to solve. You haven’t shown us the mathematical description of the relation between B and S_{1,k} and S_{2,k}. We only have your messy code. Does that result in convex optimization problem? I have no idea.

3

image
c_k is given (1,4) vector.
P is a given (4,4) diagonal matrix.
h_k is a given (1,2) vector.
A is a given (2,2) integer matrix
D is a (2,2) diagonal matrix and can be calculated easily from B as shown in the code.
p_k is a given scalar value.
From these equations, I want to find B that minimizes the difference between S2 and the given S1 (1,8) vector.
@Mark_L_Stone

4

Have you proven this is convex? Until you do, I will mark this problem as non-convex.

5

Thanks for your valuable comment. It’s non-convex. Is there any way to convert it to convex and solve it using CVX?
@Mark_L_Stone

6

There is no exact conversion to a convex problem. You can use a convex approximation, but it may not be very good.

Consider using a non-convex solver accessed via YALMIP, applied to your original problem.(more or less).