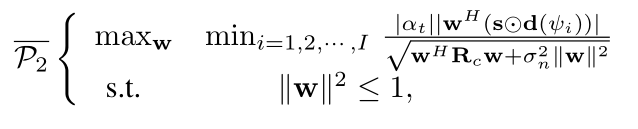
where \mathbf{w} is a column vector. As i know, |\mathbf{w}^H(\mathbf{s}\odot\mathbf{d}(\psi_i))| is a convex function with respect to \mathbf{w}, and \sqrt{\mathbf{w}^H\mathbf{R}_c\mathbf{w}+\sigma_n^2\|\mathbf{w}\|^2} is a convex function with respect to \mathbf{w}. but the objective function is nonconvex and nonconcave, i don’t know how to solve his problem.
hello, can you help me to solve this non-convex optimization?
You don’t solve it in CVX, unless as part of some higher level non-convex algorithm which calls CVX to solve convex subproblems. The design of such higher level algorithms is outside the scope of this forum.
You’d probably be better off using a non-convex solver, available for instance under YALMIP.
Thank you very much.