How can I solve this kind of large scale problem?

1

I am stuck in this problem 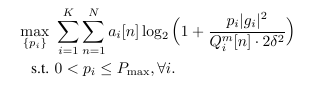Large%20problem because it is solved quite slow. My code is as following:
cvx_begin
variables pm1 pm2 pm3 pm4 pm5 pm6
maximize sum(am1.*log(1+pm1.*C1’))+sum(am2.*log(1+pm2.*C2’))+ sum(am3.*log(1+pm3.*C3’))+ sum(am4.*log(1+pm4.*C4’))+ sum(am5.*log(1+pm5.*C5’))+ sum(am6.*log(1+pm6.*C6’))
subject to
0<pm1<=P_max;
0<pm2<=P_max;
0<pm3<=P_max;
0<pm4<=P_max;
0<pm5<=P_max;
0<pm6<=P_max;
cvx_end
where C_i=|g_i|^2/{Q_i^m[n]*2*\delta^2}.

I takes a quite long time to perform the problem, Somtimes my computer even crashed due to the running so that I had to terminate it.

I think the problem results from the functions ‘log’ which requires successive approximation. So could somebody suggest an equivalent formulation that CVX can process more efficiently?

Thanks in advance.

2

Try using CVXQUAD per my April post in CVX reports unbounded status but with viable solution . You will have to rewrite log in terms of explicit exponential cone cone construct, as mentioned there (also see mvg’s answer at Solve optimization problems of exp function for reformulation).

3

Thanks a lot!

But I don’t think I completely understand your suggestion. Could you please give a further help?

4

Install CVXQUAD. Install CVXQUAD’s exponential.m replacement for CVX’s exponential.m.

For each term, log(x), replace it with an additional CVX variable z and add the constraint
{z,1,x} == exponential(1)
which models exp(z) <= x, i.e., models z <= log(x)

So you are going to have to add a lot of variables and constraints. However, I think you can vectorize the exponential cone constraints as follows:

variables x(n) z(n)
{z,1,x} == exponential(n)

rather than using n separate constraints of the form
{z(i),1,x(i)} == exponential(1)

Instead of the exponential cone construct, I believe you can use a vectroized rel_entr constraint

variables x(n) z(n)
z + rel_entr(1,x) <= 0

and this will be sufficient to invoke CVXQUAD’s Pade approximation in lieu of CVX’s successive approximation method.

I suggest you start with a simplified version of your problem to make sure everything is working correctly. Then go to the full version of your problem.

Edit: Things can be done more simply than I showed. Each instance of log(x) can be replaced by -rel_entr(1,x) without requiring any additional variables or constraints. This should work for scalar, vector, or even matrix argument o f log. That will be sufficient to invoke CVXQUAD’s Pade approximant in lieu of CVX’s successive approximation method. This still requires CVX QUAD to be installed, including its exponential.m replacement.

1 Like