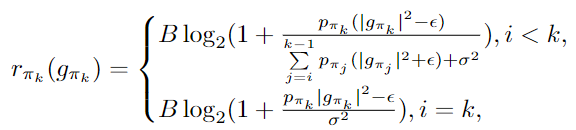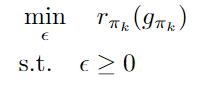How can i fix this error

Nonconvex
1

Hi, all. there is my code.

cvx_begin

variable epsilon 

expression achievable_rate_worst(K,K,K)
expression sum_interference(1,1)

for i = 1:K
    for j = 1:K
        for k = 1:K
            if i < k
                sum_interference = sum(g_k(1:k-1));
                achievable_rate_worst(i, j, k) =  B * (log(1 + (P_k * norm(g_k(1,k))^2 - epsilon) / (sum(P_k .* norm(sum_interference)^2) + sigma^2) + epsilon)) / log(2) ;
            elseif i == k
                achievable_rate_worst(i, j, k) = B * (log(1 + (P_k * norm(g_k(1,k))^2 - epsilon) / sigma^2)) / log(2) ;
            end
        end
    end
end

minimize(achievable_rate_worst(i,j,k))
subject to
epsilon >= 0;
norm(g_k(1,k))^2 - epsilon >= 0;

cvx_end

Disciplined convex programming error:
Cannot minimize a(n) concave expression.

My problem is that CVX thinks my objective function is concave.
But from the optimization problem in the graph, the objective function is convex.

2

CVX is correct. You are wrong.

Your objective is basically log(constant - epsilon) where epsilon is the variable. That is concave.

Also note that your objective consists only of the single term achievable_rate_worst(K,K,K)
which also means all the other calculations in the nested for loops are extraneous. Presumably this is not what you want. However, minimizing a concave function incurs the death penalty in CVX. You can use CVX for this problem if you forgot a minus sign in the objective function, or meant to maximize rather than minimize. Otherwise, you’re out of luck with CVX.

3

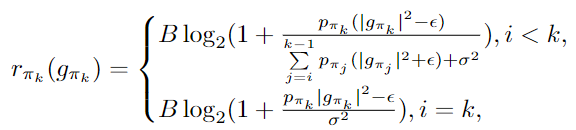
image

I want to find the code that calculates epsilon, satisfying when r is the smallest in the above expression. How should I approach this?

Or is it possible to apply Jensen inequality to the above code?

4

I don’t understand what your optimization problem is. My previous post addressed the i = k term, which is clearly concave, and is the only term in the objective function in the program you showed. I haven’t checked the i < k terms. But your description does not make clear what the relation between all these terms and your objective function is.

Because you carefully read the link in my previous post, you know your first task is to prove your optimization problem is convex. Otherwise, CVX can’t be used on it. In the event you did not carefully read that link, please do so.

5

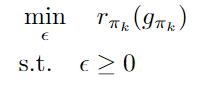
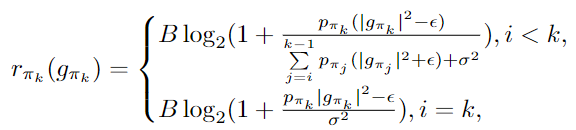
image
image

That’s my optimization problem. i think my objective function is convex…
then, i changed my code like that
for i = 1:K
for j = 1:K
for k = 1:K
if i < k
sum_interference = sum(g_k(1:k-1));
achievable_rate_worst(i, j, k) = B * (log(1 + (P_k * norm(g_k(1,k))^2 - epsilon ) / ((P_k .* norm(sum_interference)^2 + epsilon) + sigma^2) )) / log(2) ;
elseif i == k
achievable_rate_worst(i, j, k) = B * (log(1 + (P_k * norm(g_k(1,k))^2 - epsilon) / sigma^2)) / log(2) ;
end
end
end
end

occur Disciplined convex programming error: Cannot perform the operation: {real affine} ./ {real affine}

I have thoroughly read the DCP ruleset and the page you provided, but I still can’t figure out how to make modifications. If you could provide alternative guidelines, I would greatly appreciate it.

6

Did you read the part about CVX not be suited for all optimization problems?

7

Yes, I read that part. now…i am looking for other ways such as fmincon.