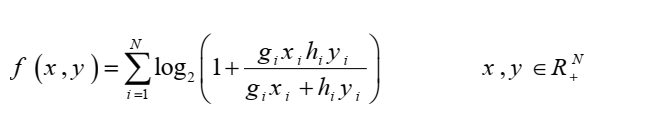
this is a concave function f = hog that g and h is concave and nondecreasing
I wrote this code but I get an Error
cvx_begin
variable x(N,1) nonnegative
variable y(N,1) nonnegative
variable obj
expression R(N,1)
for r = 1 : N
R( r)=log2(1+ (g( r) *x( r)*h( r)*y( r))/(g( r)*x( r)+h(r )*y(r )));
end
maximise sum(R );
cvx_end
Clearly restrictions are needed on g_i and h_i. For instance, if N = 1, g_1 = -1, h_1 = 1, x=1, y = 2, then the Hessian of the function has one negative eigenvalue and one positive eigenvalue; so the function is not concave there.
Presuming suitable restrictions are placed on g_i and h_i so as to ensure concavity, I will leave it to someone else to determine if it can be reformulated for CVX.
Have you read the CVX User’s Guide http://cvxr.com/cvx/doc/ ? If so, you should be aware that you need to follow CVX’s rules, which your program doesn’t.
Why isn't CVX accepting my model? READ THIS FIRST!
And also, that log2 is not supported by CVX; so you must either use log(...)/log(2) , or don’t bother with dividing by log2 if this appears as a multiplicative factor for the entire objective function (and then divide the resulting optimal objective value by log(2) ).
thank you
we have
gi=1 and hi =1 for all i
the only constraint is
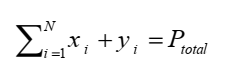
that is affine
If everything is of appropriate signs then the fraction inside the logarithm is the (rescaled) harmonic mean of x_i,y_i which has conic models in https://docs.mosek.com/modeling-cookbook/cqo.html#harmonic-mean
very thank you sir
your guide and this link was usefull
and log is increasing function
i wrote this code then and solved
clear all;close all;clc
N = 10;
g = 1;
h = 1;
r = 1;
ObjValue = zeros(4,1);
for i = 1 : N
cvx_begin
variable x nonnegative
variable y nonnegative
minimize inv_pos(h*y)+inv_pos(g*x)
subject to
x + y == Pt
cvx_end
if ~exist('f', 'var') || isempty(f)
f = log2(1+1/cvx_optval);
else
f = [f,log2(1+1/cvx_optval)];
end
end
ObjValue(r) = sum(f);
Your code seems to e solving a very different problem than you originally provided. The argument of log is different. And taking the log after the optimization is completed will not be equivalent when N > 1.
You should follow the guidance provided by @Michal_Adamaszek
thank i wrongly think that constraint is separatable.
in fact harmonic mean is in the argument of log and is difficult to express this for CVX
If you use the harmonic mean from th link then there is no problem
maximize \sum_i \log(1+u_i)
such that u_i\leq \mathrm{harmonic}(g_ix_i,h_iy_i) (times some constants maybe)
is the conic model.
thank you, I wrote this and I get an error
Error using .* (line 173)
Disciplined convex programming error:
Cannot perform the operation: {positive constant} ./ {real affine}
Error in ./ (line 19)
z = times( x, y, ‘./’ );
Error in harmmean (line 28)
m = 1 ./ mean(1./x, varargin{:});
Error in Q2 (line 21)
u <= harmmean([g.*x,h.*y],2)
N = 10;
g = ones(N,1);
h = ones(N,1);
cvx_begin
variable x(N,1) nonnegative
variable y(N,1) nonnegative
expression u(N,1)
maximise sum_log(1+u)
subject to
u <= harmmean([g.*x,h.*y],2)
sum(x + y) == 5
cvx_endBy harmean I mean the model you will get if you implement any of the conic formulations from https://docs.mosek.com/modeling-cookbook/cqo.html#harmonic-mean I didn’t suggest there is a ready function for it.