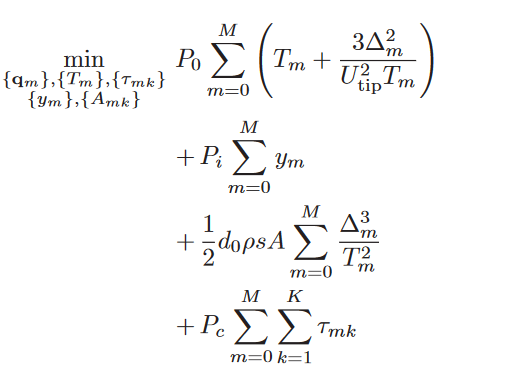
\delta_m^2/T_m can be handled by the quad_over_lin function, but how can I deal with the third part: \delta_m^3/T_m^2, while delta_m (delta_m = |q_{m+1}-q_m|) is convex and T_m is affine? Thank you~
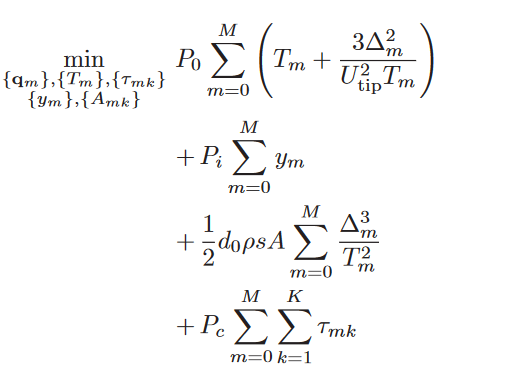
\delta_m^2/T_m can be handled by the quad_over_lin function, but how can I deal with the third part: \delta_m^3/T_m^2, while delta_m (delta_m = |q_{m+1}-q_m|) is convex and T_m is affine? Thank you~
Assume you have
and
then that implies
There is a geometric mean function in cvx.
Thank you very much, your answer is beneficial.