I have an optimization problem contains erf() in the constraint. The optimization problem is convex. As I checked cvx does not have erf(), how can I add this function to cvx.
Thanks.
erf(x) is convex for x < 0, concave for x > 0. So erf can’t be added as a function to CVX, unless it is restricted to positive, or separately, negative.argument, and even then, i don’t know how to do it, or even whether it can be done.
Please show us the constraint containing erf, and the proof that the constraint is convex,
Thanks for your response,
to make it simple, consider x and v1 are constant vectors, my constraint is in the form of
t - log(1+ 0.5 * erf(0.1* real(x’ *(v-v1)) + 0.2)) <= 0 ;
where v is a vector and we know that the argument of erf() is positive. Here, v and t are optimization variables and t>0.
As erf(y) is concave for y>0 and log() is also a concave and non decreasing function, hence the constraint is convex respect to t and v.
Thanks.
At
you find some approximations of the error function. Maybe you can use some of those to solve a good approximation of your problem.
Further to @Erling 's point, one such approximation has already been implemented in CVX.
In particular, I believe you can reformulate the constraint in question using log of the standard Normal cumulative distribution function. Then use CVX’s log_normcdf
http://cvxr.com/cvx/doc/funcref.html#new-functions
log_normcdf(x)
logarithm of cumulative distribution function of standard normal random variable. Concave and increasing. The current implementation is a fairly crude SDP-representable approximation, with modest accuracy over the interval [−4,4]; we intend to replace it with a much better approximation at some point
BTW, I think “some point” is now the point at infinity.
help log_normcdf
log_normcdf Logarithm of the cumulative normal distribution.
Y = log_normcdf(X) is the logarithm of the CDF of the normal
distribution at the point X.1 / x log_normcdf(X) = LOG( ------- | exp(-t^2/2) dt ) sqrt(2) / -Inf For numeric X, log_normcdf(X) is computed using the equivalent expression LOG(0.5*ERFC(-X*SQRT(0.5))). When X is a CVX variable, a a piecewise quadratic *approximation* is employed instead. This approximation gives good results when -4 <= x <= 4, and will be improved in future releases of CVX. For array values of X, the log_normcdf returns an array of identical size with the calculation applied independently to each element. X must be real. Disciplined convex programming information: log_normcdf is concave and nondecreasing in X. Therefore, when used in CVX specifications, X must be concave.
Thanks for your response, I have tried some of the approximations, however cvx can not handle the new constraint with approximate erf().
Thanks, I will give it a try.
In my case, x is complex.
I have also tried to solve the problem using fmincon. However, I do not know why the solution of fmincon is not the optimum one.
I considered a similar optimization problem that could be solved through CVX. I solved the problem through cvx and aslo fmincon. But cvx gives me the correct solution which is not similar to the solution of fmincon. I do not know what is wrong with fmincon. Do you have any idea on that?
Thanks.
x being complex shouldn’t matter here. Your constraint uses the real part of the expression involving x, so a real argument will be presented to log_normcdf.
We have no idea what you did with FMINCON, or what its output and reported solution status were. If the overall problem is convex and if you did not make a coding mistake, and if FMINCON reports that is has found a solution satisfying first order conditions, and if FMINCON didn’t get screwed up by bad numerics, and if FMINCON plus whatever tool, if any, you used to call it, don’t have bugs (that’s a lof of ifs), then the FMINCOM solution should be the global minimum, within tolerance.
.
Thanks for your response and your time. Here is a simple problem ,
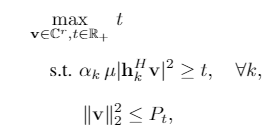
The matlab codes that use fmincon and cvx are as follows,
clc;
clear all;
close all;
%% Initial values
K = 2 ;
H =[ -0.0051 - 0.0430i, -0.1206 - 0.0879i;
0.0158 - 0.1206i -0.0949 - 0.0916i];
alpha_k = 1.0e+03 * [7.3293 ; 5.6856];
p = 3.1623;
mu = 0.1109;
optimal_v1 = opt_fmin(K,H,alpha_k,mu, p) ; % optimization using fmincon
optimal_v2 = opt_cvx(K,H,alpha_k,mu, p) ; %optimization using cvx
abs(optimal_v2 - optimal_v1)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [v_optimal] = opt_fmin(K,H,alpha_k,mu, p_t)
z = sqrt(0.5)*complex(randn(K,1),randn(K,1));
z1 = z/norm(z) ;
v_hat = sqrt(p_t) * z1; %intitial value for v
max_iter = 50 ;
for ind_conv = 1:max_iter
fun = @(x)-x(1);
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
option = optimset(‘Display’,‘on’,‘Algorithm’,‘interior-point’,'TolFun ',1e-15,‘TolCon’,1e-15,‘TolX’,1e-15,‘TolCon’,1e-15);
x0 = [0;0;0;];
x0(2)=v_hat(1);
x0(3)=v_hat(2);
v1 = v_hat;
a_temp = alpha_k(1,1) * mu * (quad_form(v_hat,H(:,1)H(:,1)’)+ 2 * real(v_hat’ H(:,1) * H(:,1)’ *(v1-v_hat))) ;
b_temp = alpha_k(2,1) * mu * (quad_form(v_hat,H(:,2)H(:,2)’)+ 2 * real(v_hat’ H(:,2) * H(:,2)’ *(v1-v_hat))) ;
x0(1) = min([a_temp,b_temp]);
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,@(x)unitdisk(x,H,v_hat,alpha_k,p_t,mu),option);
v_optimal = [x(2);x(3)];
if (abs(v_optimal - v_hat)< 1e-6)
break ;
end
v_hat = [x(2);x(3)];
end
end
function [c,ceq] = unitdisk(x,H,v_hat,alpha_k,p_t,mu)
t=x(1);
v=[x(2);x(3)];
c = [t(1)- alpha_k(1,1) * mu * (quad_form(v_hat,H(:,1)H(:,1)’)+ 2 * real(v_hat’ H(:,1) * H(:,1)’ *(v-v_hat)));
t(1)- alpha_k(2,1) * mu * (quad_form(v_hat,H(:,2)H(:,2)’)+ 2 * real(v_hat’ H(:,2) * H(:,2)’ *(v-v_hat))) ;
(v’ * v) - p_t;];
ceq = [];
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [v_optimal] = opt_cvx(K,H,alpha_k,mu, p_t)
z = sqrt(0.5)*complex(randn(K,1),randn(K,1));
z1 = z/norm(z) ;
%
v_hat = sqrt(p_t) * z1; %intitial value for v
max_iter = 100 ;
for ind_conv = 1:max_iter
cvx_begin quiet
variable v(K,1) complex
variable t(1)
maximize(t)
subject to
t- alpha_k(1) * mu * (quad_form(v_hat,H(:,1)H(:,1)’)+ 2 * real(v_hat’ H(:,1) * H(:,1)’ *(v-v_hat))) <= 0 ;
t- alpha_k(2) * mu * (quad_form(v_hat,H(:,2)H(:,2)’)+ 2 * real(v_hat’ H(:,2) * H(:,2)’ *(v-v_hat))) <= 0 ;
(v’ * v) <= p_t;
cvx_end
v_optimal = v ;
if (abs(v_optimal - v_hat)< 1e-6)
break ;
end
v_hat = v;
end
end
You have totally lost me. Where is there an erf or log in rhe problem you just presented?
it really helps to have a consistent exposition, with formulation and results of various solution methods or software pertaining to a common problem. It helps readers. Most importantly, it helps you discover your own inconsistencies.
This is not an FMINCON forum, so I won’t provide a detailed review of your code. But I will note that it makes little sense for you to apply SCA, using FMINCON to solve convex subproblems. You should instead just call FMNCON to solve the original non-convex problem. Whether using SCA or FMINCON, you will not be guaranteed to find global optimum (or loval optimum, or anything).
Your crude SCA implementation, not having the (global) convergence benefit of safeguarding by use of trust regions or line search, is not guaranteed to converge to anything, let alone a global or even local optimum of the original problem. it is a poor man’s non-convex nonlinear optimizer, a very bad one at that. There is a reason that the FMINCON source code is not 10 lines long.
You are not solving a convex problem. Any solution you obtain is not guaranteed to be a global optimum unless obtained by a (rigorous) global optimizer, such as BARON or YALMIP’s BMIBNB.
Both FMINCON and SCA may be very sensitive to choice of starting values for the variables.
Thanks, you are right. Sorry about that. I just wanted to figure out the problem with fmincon, and I needed to find a problem that could be solved by both cvx and matlab toolbox. I thought a simple problem may be easier to follow.
So do you recommend me to use BARON or YALMIP’s BMIBNB to solve such problems that may also contain erf() . I mean in the main problem I have just presented, the first constraint be replaced with
\alpha_k erf(a|h_k’ v|^2+b) >= t, where the argument of erf() is positive.
Thanks,
You can try solving it with BMIBNB, which needs to call an upper solver to locally solve nonlinear subproblems. FMINCON is one such upper solver which can be called by BMIBNB.
erf is not a function “known” to BARON.
I don’t want to speak ill of Stephen Boyd, but his presentation of crude SCA solvers applied to problems and starting values for which it works well, gives people the wrong impression about how well it is likely to work on other problems, especially if you don’t happen to be Stephen Boyd, whose abilities vastly exceed those of the average person who attempts SCA…
Thanks for your help. I will try this.
I am trying to solve the problem with YALMIP’s BMIBNB.
I have two problems,
- The optimum value of v is real. However, I do not know how to declare v as a complex vector.
2- I want to use the optimum value of v to calculate some equations, but I can not do so. for instance if v be a vector ( 2*1), I want to have
y = log(v - [1 ; 3]);
Could you please help me to figure it out.
Following is the code:
sdpvar v(2,1);
sdpvar t;
Constraints = [t- alpha_k(1) * mu * (quad_form(v,H(:,1)*H(:,1)‘))<=0,
t- alpha_k(2) * mu * (quad_form(v,H(:,2)*H(:,2)’))<=0,
(v’ * v) - p_t <= 0];
Objective = -t
options = sdpsettings(‘solver’,‘bmibnb’,‘bmibnb.uppersolver’,‘fmincon’);
optimize(Constraints,Objective,options) % solve the problem
Yes, I can figure it out, as I am quite experienced in YALMIP. But this is not the appropriate forum for YALMIP or BMIBNB help. I advise you to read the tutorial info on YALMIP, starting with https://yalmip.github.io/tutorial/basics/ and https://yalmip.github.io/command/sdpvar/ , which should address the difficulties you’re having. Then only after doing that, ask for help at https://groups.google.com/forum/?fromgroups#!forum/yalmip if needed.
Sure. Thanks for your response.
I’ll give you one helpful tip, because it will also help people using CVX.
Don’t use CVX functions, such as quad_form on YALMIP expressions.
Don’t use YALMIP functions, such as cpower on CVX expressions.
This does not apply to functions which are overloaded for both CVX and YALMIP expressions, although you need to observe the syntax and restrictions applicable to what you do apply it to.
A month ago, there was a post on this forum of someone applying a CVX function, inv_pos to a YALMIP expression How to deal with the SDP problem with nonlinear constraint? . That didn’t go well.
@sheida I suggest you delete your YALMIP forum post using quad_form so that you don’t waste Johan’s time with that. He’;s in Sweden, so you probably have at least 5 hours to replace it with a better formulated post.before he sees it. I have toi admit though, there’s a part of me that wants to see his reaction to quad_form being applied to a YALMIP expression in a constraint.
Thanks for the hint. I did so.