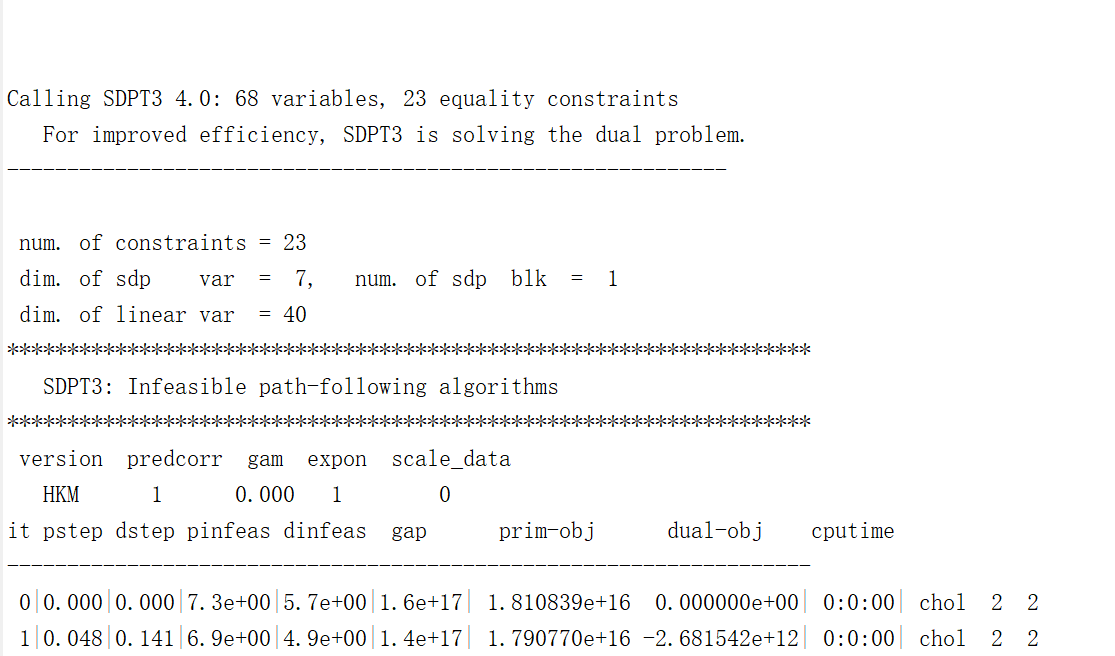
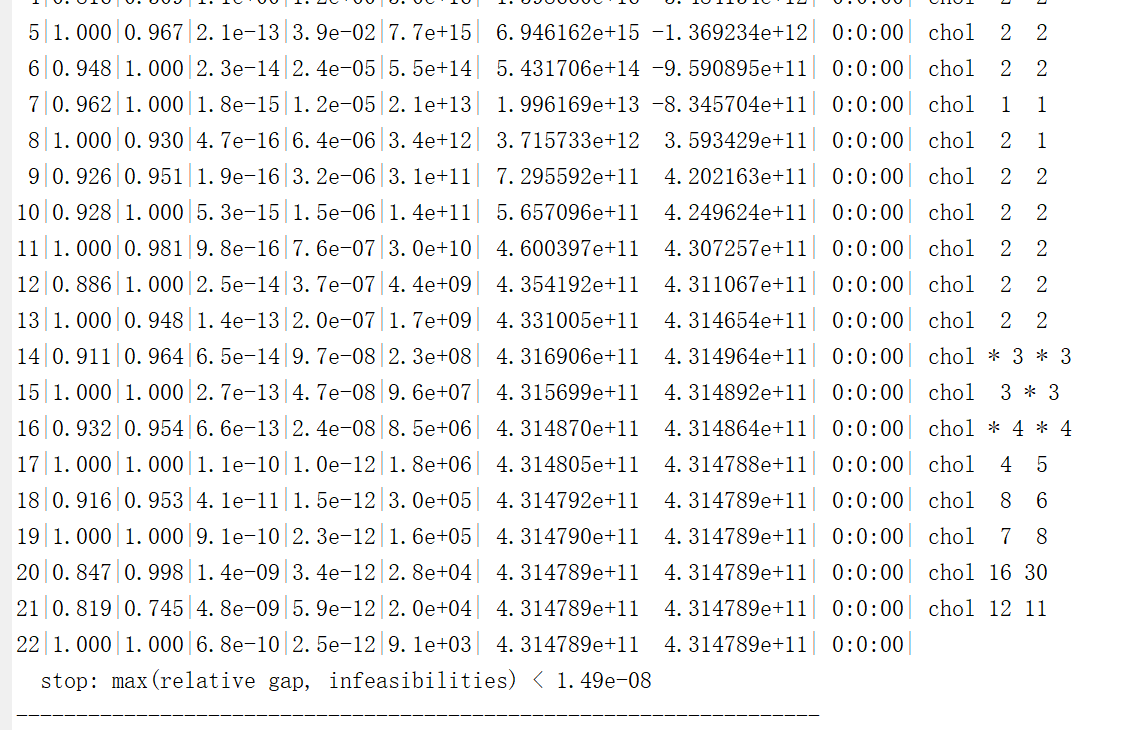
the following is my code, which is a SDP problem, however, the result shows “Status: Unbounded”.
I want to know why this happens.
clc
clear all
close all
%% 测量点位置
Radius=1.500;
Angle=linspace(0,2pi,30);
PosLoc=[Radiuscos(Angle(1:end-1));Radiussin(Angle(1:end-1))];
PosLoc=PosLoc’;
xShip=PosLoc(:,1)+1000.001randn(size(PosLoc(:,1)));
yShip=PosLoc(:,2)+1000.001*randn(size(PosLoc(:,1)));
zShip=0; % 发射换能器的入水深度
%% 目标位置
Range=600;[200:100:1000];
xTar=0.001Range/sqrt(2);
yTar=0.001Range/sqrt(2);
NN=length(Range); % 阵元数目
zTar=0;
%% 添加测量误差
detat=1*0.001; % 时延测量误差
c0=1.500;
detac=010.001; % 声速测量误差
detaa=010.001; % 节点位置的随机误差
T0=5;
%% 主程序
for nn=1:NN
nn
for mc=1:1
%%%% 构造带误差的测量值
xShipMea=xShip+detaa*randn(size(xShip));
yShipMea=yShip+detaa*randn(size(yShip));
tMea=sqrt((xShip-xTar(nn)).^2+(yShip-yTar(nn)).^2+(zShip-zTar).^2)/c0+detat*randn(size(xShip))+(0:length(xShip)-1)'*T0;
c=c0+detac*randn;
%%% 主程序
s=[xShipMea(2:end)-xShipMea(1),yShipMea(2:end)-yShipMea(1)];
t=tMea(2:end)-tMea(1);
M=length(t);
h1=sum(s.^2,2)-t.^2*c^2;
A1=2*s;
N=(1:M)';
B1=[2*t*c,-2*N*c,-2*N.*t*c^2,N.^2*c^2];
Qt=detat^2*(ones(length(tMea)-1)+eye(length(tMea)-1));
W=eye(M);
for it=1
F=[A1 B1];
PHI=[F'*W*F,-F'*W*h1;
-h1'*W*F,h1'*W*h1];
cvx_begin sdp
variable y(6,1);
variable Y(6,6);
minimize(trace([Y,y;y',1]*PHI));
subject to
[Y,y;y',1]==semidefinite(7);
Y(1,1)+Y(2,2)-Y(3,3)==0;
Y(3,5)-y(4)==0;
Y(5,5)-y(6)==0;
Y(3,6)-Y(4,5)==0;
% norm(Y(1,1)+Y(2,2)) <= y(3);
%
% norm(Y(1,5)+Y(2,5)) <= y(4);
%
% norm(Y(1,6)+Y(2,6))<=Y(3,6);
cvx_end
xFinal=y(1);
yFinal=y(2);
TFinal=y(5);
C1=-2*diag(sqrt((xFinal-s(:,1)).^2+(yFinal-s(:,2)).^2));
W=eye(M)/(C1*Qt*C1');
end
xFinal=xFinal+xShipMea(1);
yFinal=yFinal+yShipMea(1);
xSDR(mc,nn)=xFinal;
ySDR(mc,nn)=yFinal;
end
end
%%% 均方根误差
RmseSDR=1000*sqrt(sum((xSDR-ones(mc,1)*xTar).^2+(ySDR-ones(mc,1)*yTar).^2,1)/mc);
%%%% 估计偏差
BiasSDR=1000*sqrt((mean(xSDR-ones(mc,1)*xTar,1)).^2+(mean(ySDR-ones(mc,1)*yTar,1)).^2);
%% 绘图和保存数据
figure;
hold on
scatter(1000xShip,1000yShip,‘blue.’);
scatter(1000xTar,1000yTar,‘red.’);
legend(‘水面船航路’,‘海底阵阵元’)
xlabel(‘x(m)’);
ylabel(‘y(m)’);
xlim([-2000 2000])
ylim([-2000 2000])
axis equal
grid on
box on
name=‘几何态势图’;
% SavePicture( gcf,name,0 );
figure;
hold on
plot(Range,RmseSDR,‘red-*’,‘LineWidth’,1.5)
box on
grid on
set(gca,‘GridLineStyle’,‘–’)
xlabel(‘海底阵阵元和原点之间的水平距离(m)’)
ylabel(‘海底阵阵元位置的均方根误差(m)’)
name=‘均方根误差’;
figure;
hold on
plot(Range,BiasSDR,‘red-*’,‘LineWidth’,1.5)
box on
grid on
set(gca,‘GridLineStyle’,‘–’)
xlabel(‘海底阵阵元和原点之间的水平距离(m)’)
ylabel(‘海底阵阵元位置的估计偏差(m)’)
name=‘估计偏差’;
% SavePicture( gcf,name,0 );