Help! Some problem with "kron"

[Xiaoqi (Xiaoqi Wang)]

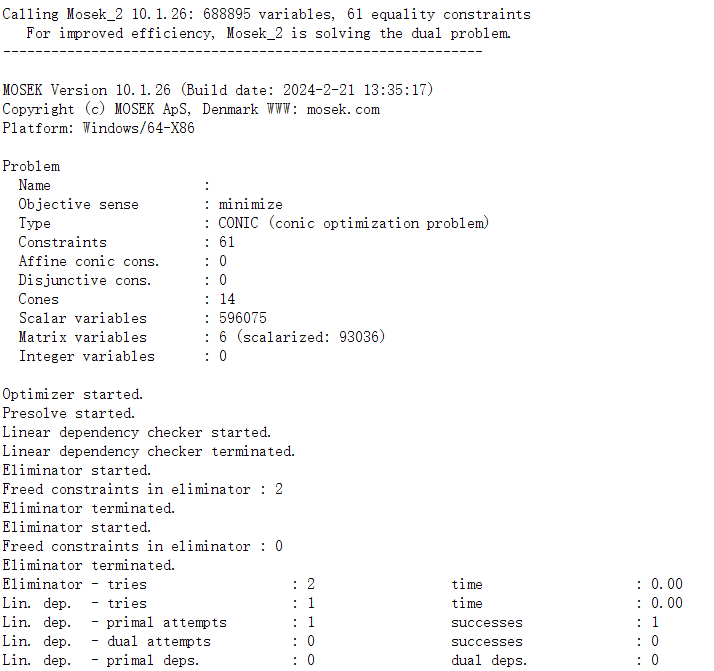
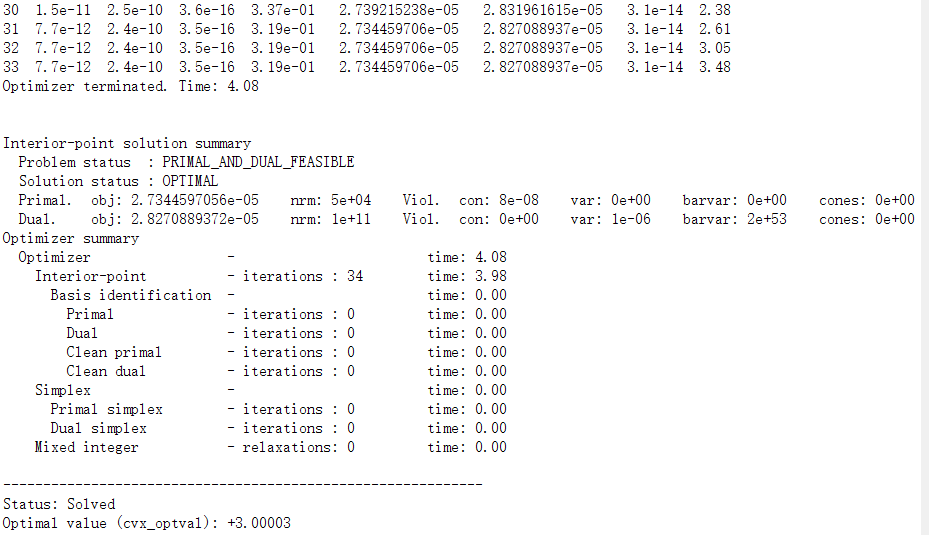
Hello! I’m trying to solve the conic optimization problem with Mosek. My code and the output is below. The matrix variable W is a set of complex matrixes. No matter how I change the parameters and units, the result is too small, and W is a real matrix. The problem seems to be with Q(:,:,k) = kron(W(:,:,k)',V); because when I remove the kron operation, the result is normal. (V is a constant matrix.) Do you have any suggestions for me? Thank you so much!

max_iteration = 10;

lamda = ones(param.K,param.K);
tau = zeros(param.K,1);
rho = log(1/param.pout);

for ite = 1:max_iteration
cvx_solver mosek_2
cvx_begin
variable W(param.Nt,param.Nt,param.K) complex
variable delta(param.K,1) nonnegative
variable omega(param.K,param.K) nonnegative
variable t(param.K,1) nonnegative
variable miu(param.K,1)
variable upsilon(param.K,1) nonnegative

    expression Q(param.Nt*(param.N+1),param.Nt*(param.N+1),param.K)
    expression R(param.Nt*(param.N+1),1)
    expression c(param.K,1)

    maximize (sum(delta))

    subject to
        % semidefinite
        for k = 1:param.K
            W(:,:,k) == hermitian_semidefinite(param.Nt);
        end

        % power
        real(trace(sum(W,3))) <= param.Pmax;
        
        % secrecy rate
        for k = 1:param.K
            1+omega(k,k)-tau(k)*(1+t(k)) >= delta(k);
        end

        % SOP
        for k = 1:param.K
            Q(:,:,k) = kron(W(:,:,k)',V);
            R(:,k) = Q(:,:,k)*vec(param.Ge_hat);
            c(k) = t(k)*param.Pnoise-real(vec(param.Ge_hat)'*R(:,k));
            real(trace(Q(:,:,k)))+sqrt(2*rho)*miu(k)+rho*upsilon(k)-c(k) <= 0;
            real(norm([vec(Q(:,:,k));sqrt(2)*R(:,k)])) <= miu(k);
            upsilon(k)*eye(param.Nt*(param.N+1))-Q(:,:,k) == semidefinite(param.Nt*(param.N+1));
        end

        % NOMA SR
        for k = 1:param.K
            for j = k:param.K
                x = omega(j,k);
                y = real(trace(sum(W(:,:,k+1:end),3)*param.Gc(:,:,j)'*V*param.Gc(:,:,j)))+param.Pnoise;
                pow_p(lamda(j,k)*x,2)+pow_p(y/lamda(j,k),2) <= 2*real(trace(W(:,:,k)*param.Gc(:,:,j)'*V*param.Gc(:,:,j)));
                omega(j,k) >= omega(k,k);
            end
        end

        % NOMA power
        for k = 1:param.K
            for i = 1:param.K
                for j = i+1:param.K
                    real(trace(W(:,:,i)*param.Gc(:,:,k)'*V*param.Gc(:,:,k))) >= real(trace(W(:,:,j)*param.Gc(:,:,k)'*V*param.Gc(:,:,k)));
                end
            end
        end
cvx_end

% update param
if contains(cvx_status,'Solved')
    for k = 1:param.K
        tau(k) = (1+omega(k,k))/(1+t(k));
        for j = k:param.K
            x = omega(j,k);
            y = real(trace(sum(W(:,:,k+1:end),3)*param.Gc(:,:,j)'*V*param.Gc(:,:,j)))+param.Pnoise;
            if x == 0
                lamda(j,k) = lamda(j,k);
            else
                lamda(j,k) = sqrt(y/x);
            end
        end
    end
end   

end

This is the result of W

[Michal_Adamaszek]

I have no comment about kron, but you are welcome to dump the task file of that problem (instructions in 1 Technical Issues — MOSEK FAQ 10.1.28) and send to Mosek support. I find that solution summary very intriguing, as you can see there is something numerically very nasty going on with the matrix variable value (barvar: 2e+53). Another thing is that your dual solution seems to have very large norm, which means your primal CVX solution is expected to be huge and that is not good from a modeling point of view.

[Xiaoqi (Xiaoqi Wang)]

Thank you for your reply! I’ll try for that and maybe I need to make more adjustment to my model scale.