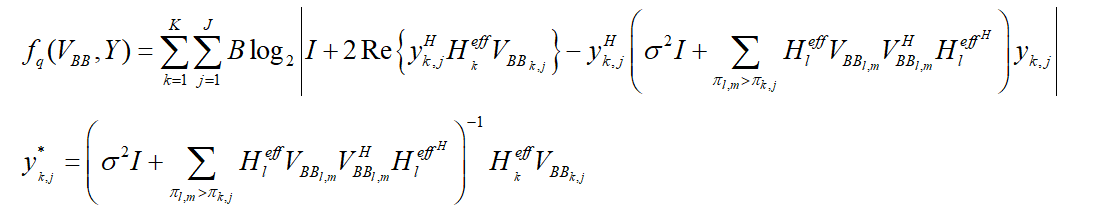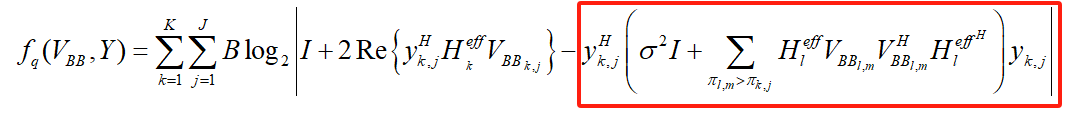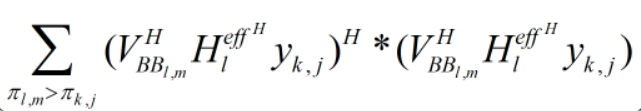HELP！I don't know how to solve this problem

1

y = updateY(K,J,Nr,Ns,h_eff,noise,decodingorder,VBB); % Calculate the optimal value of auxiliary variable ym

    % Using CVX to solve convex optimization problems for optimizing power allocation {pkj}
    cvx_begin quiet
        cvx_solver mosek
            variable VBB(Nrf, Ns, K, J) complex % The power of each sub message
            expressions fq_r(K,J)  interference(Nr,Nr,K,J)% The rate of each sub message and user interference

            for k = 1:K
                for j = 1:J

                    [row,col] = find(decodingorder>decodingorder(k,j)); % Identify data streams that decoding order greater as interference
                
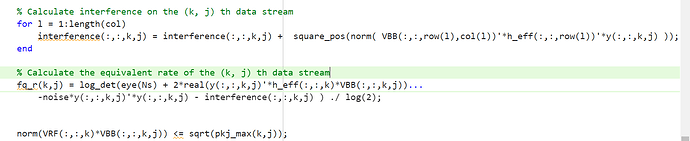
                    % Calculate interference on the (k, j) th data stream
                    for l = 1:length(col)
                        interference(:,:,k,j) = interference(:,:,k,j) +  square_pos(norm(h_eff(:,:,row(l)) * VBB(:,:,row(l),col(l))));

% h_eff(:,:,row(l)) * VBB(:,:,row(l),col(l)) * VBB(:,:,row(l),col(l))’ * h_eff(:,:,row(l))';
end

                    % Calculate the equivalent rate of the (k, j) th data stream
                    fq_r(k,j) = log_det(eye(Ns) + 2*real(y(:,:,k,j)'*h_eff(:,:,k)*VBB(:,:,k,j))...
                        -y(:,:,k,j)'*(interference(:,:,k,j) + noise*eye(Nr))*y(:,:,k,j)) ./ log(2);


                    norm(VRF(:,:,k)*VBB(:,:,k,j)) <= sqrt(pkj_max(k,j));
                    sum(sum_square_abs(VBB(:,:,k,j))) <= pkj_max(k,j);
                    
                end
            end
            maximize sum(fq_r(:)) % objective function Q_sumrate
            subject to
                fq_r >= r_min; % Minimum data stream rate requirement
    cvx_end

There is a erro：
错误使用 &
操作数必须为实数。

出错 cvx/cvx_vexity (第 38 行)
v( any( imag( x.basis_ ), 1 ) & v ) = NaN;

出错 * (第 296 行)
v = cvx_vexity( z );

出错 get_VBB_runFP (第 66 行)
-y(:,:,k,j)'(interference(:,:,k,j) + noiseeye(Nr))*y(:,:,k,j)) ./ log(2);

Perhaps CVX does not support matrix multiplication like A '* B * A. Is there any other equivalent conversion method that CVX can handle?

2

image
image1104×210 7.42 KB

3

What are the dimensions of A and B? Which are input data? Do you have a factorization of B as C*C’?

4

My original question is Maximize Σ log (1+SINR). Transforming the problem into fq (V, Y) through fractional programming（You can see from the pictures in my comments）, when Y is given, fq is a convex optimization problem. In this convex optimization problem, there is a term similar to A '* B * A, where the dimension of matrix A is Nr x Ns, and B is Nr x Nr

5

What is the specific term you are having difficulty formulating in CVX? Make clear the dimensions of everything, what are variables and what is input data. Also, please supply the convexity proof.

6

1712064926602
17120649266021081×115 5.18 KB

The convex optimization problem aims to maximize fq. The variables are only VBB, and all other matrices are known. The problem lies in the expression within the red box. The dimension of matrix y is Nr x Ns, H is Nr x Nrf, and VBB is Nr fx Ns

7 
x  = V'*H'*y;
x'*x

Or

 (V'*H'*y)'*(V'*H'*y)

I’ll let you add in the indexing and make it into a sum.

8

Sorry, I didn’t understand what you meant. Do you mean to turn the item in the red box into this?
image

9

Yes, plus of course the sigma^2*y'*y term

10

Okay, I’ll give it a try. I am not very good at matrix operations. Thank you very much！

11

There is a new error now.

image
image1521×342 11 KB

Error corresponds to this item in the expression.
image
image1065×104 5.08 KB

12

Did you forget to apply real(...) to the term which CVX says is complex affine?

13

image
image1515×310 33.3 KB

I use real

14

You did not apply real to noise. Is that complex?

15

Now my program is like this：

image
image939×105 10.4 KB

The error is as follows:
image
image1517×465 15.9 KB

16

Is the argument of log_det hermitian semidefinite?

17

yeah, The matrix in log_det is positively definite.

18

I don’t know what all the input data is, but that claim is not obvious to me.

Perhaps you can explicitly type the argument of log_det using Preformated text (don’t show an image) and prove it is hermitian semidefinite. When doing so, make clear what the dimensions of everything are. Please take your time to do this systematically and carefully, rather than rushing to post again.

19

Okay, thank you for your reply！