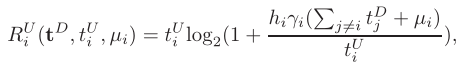
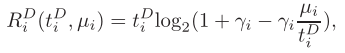
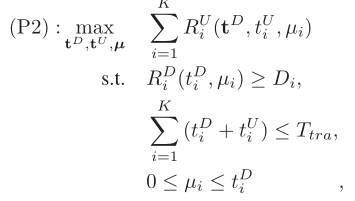
This is my code.
T_tra=1;D=[0.5,0.4,0.8,0.3,0.2];Y=[4,5,5.5,9,10];h=0.001Y.^(-2);
P_BS=30;NP=-50;gamma=P_BSh/NP;
Delta=0.01;
cvx_begin gp
variable t_D(1,5) nonnegative;variable t_U(1,5) nonnegative; variable miu(1,5);
expression r_U(1,5);
for i=1:5
r_U(1,i)=t_U(1,i)*log(1+(h(1,i)gamma(1,i)(sum(t_D)-t_D(1,i)+miu(1,i)))/t_U(1,i))/log(2);
end
maximize(r_U)
subject to
for i=1:5
t_D(1,i)*log(1+gamma(1,i)-gamma(1,i)*miu(1,i)/t_D(1,i))/log(2)>=D(1,i);
sum(t_D)+sum(t_U)<=T_tra;
0<=miu(1,i)<=t_D(1,i);
end
cvx_end
but it has a error

how to solve this?
Expressions of the form
x*log2(1+y/x)
can be entered into CVX as
-rel_entr(x,x+y)/log(2)
presuming that x is a variable, or affine (linear) function of a variable, and `Y`` is concave (which includes a variable or linear (affine) function of a variable as special cases).
The superscripts D are apparently indices, not exponents. Therefore, this reformulation should work on your problem.
help rel_entr
rel_entr Scalar relative entropy.
rel_entr(X,Y) returns an array of the same size as X+Y with the
relative entropy function applied to each element:
{ X.*LOG(X./Y) if X > 0 & Y > 0,
rel_entr(X,Y) = { 0 if X == 0 & Y >= 0,
{ +Inf otherwise.
X and Y must either be the same size, or one must be a scalar. If X and
Y are vectors, then SUM(rel_entr(X,Y)) returns their relative entropy.
If they are PDFs (that is, if X>=0, Y>=0, SUM(X)==1, SUM(Y)==1) then
this is equal to their Kullback-Liebler divergence SUM(KL_DIV(X,Y)).
-SUM(rel_entr(X,1)) returns the entropy of X.
Disciplined convex programming information:
rel_entr(X,Y) is convex in both X and Y, nonmonotonic in X, and
nonincreasing in Y. Thus when used in CVX expressions, X must be
real and affine and Y must be concave. The use of rel_entr(X,Y) in
an objective or constraint will effectively constrain both X and Y
to be nonnegative, hence there is no need to add additional
constraints X >= 0 or Y >= 0 to enforce this.
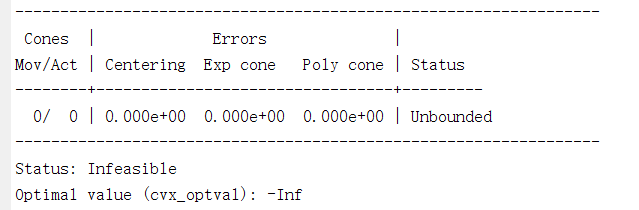 Thanks! I have successfully solved this problem through this method. But there is another problem.
Thanks! I have successfully solved this problem through this method. But there is another problem.
If you have Mosek 9.x available, i recommend you use that (latest version of Mosek 9.2.x) as solver. If not, install CVXQUAD’s exponential.m replacement, and follow the instructions at CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions .
After doing that, if the result is still infeasible, follow the guidance at https://yalmip.github.io/debugginginfeasible/ , all of which also applies to CVX, excpet for section 1.
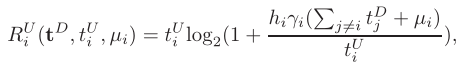
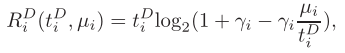
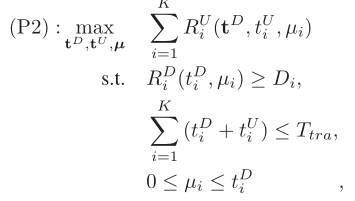

 Thanks! I have successfully solved this problem through this method. But there is another problem.
Thanks! I have successfully solved this problem through this method. But there is another problem.